The A.I Megathread (LLM , GPT , Development)
1/4
OpenAI's Noam Brown says the o1 model's reasoning at math problems improves with more test-time compute and "there is no sign of this stopping"
2/4
Source:
https://invidious.poast.org/watch?v=Gr_eYXdHFis
3/4
yes, it's a semi-log plot with the log scale on the x-axis, so it doesn't scale linearly, but Noam does state this
4/4
as I understand it, the primary reasoning domains o1 is trained on are math and coding. literature is more within the ambit of the GPT series.
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
OpenAI's Noam Brown says the o1 model's reasoning at math problems improves with more test-time compute and "there is no sign of this stopping"
2/4
Source:
https://invidious.poast.org/watch?v=Gr_eYXdHFis
3/4
yes, it's a semi-log plot with the log scale on the x-axis, so it doesn't scale linearly, but Noam does state this
4/4
as I understand it, the primary reasoning domains o1 is trained on are math and coding. literature is more within the ambit of the GPT series.
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/2
Stuart Russell: saying AI is like the calculator is a flawed analogy because calculators only automate the brainless part of mathematics whereas AI can automate the essence of learning to think
2/2
Source (thanks to @curiousgangsta):
https://invidious.poast.org/watch?v=NTJK5e9ADcw
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Stuart Russell: saying AI is like the calculator is a flawed analogy because calculators only automate the brainless part of mathematics whereas AI can automate the essence of learning to think
2/2
Source (thanks to @curiousgangsta):
https://invidious.poast.org/watch?v=NTJK5e9ADcw
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/11
@tsarnick
Stuart Russell says by the end of this decade AI may exceed human capabilities in every dimension and perform work for free, so there may be more employment, it just won't be employment of humans
https://video-t-1.twimg.com/ext_tw_...9152/pu/vid/avc1/720x720/ktlc06x_refu7Bd2.mp4
2/11
@tsarnick
Source (thanks to @curiousgangsta):
https://invidious.poast.org/watch?v=NTJK5e9ADcw
3/11
@ciphertrees
I think everyone will be employed doing something they want to do in the future. You might work at a car plant building cars that people don't actually buy. Drive around with your coworkers later in the cars you just made?
4/11
@0xTheWay
Maybe there will be an enlightenment period where we aren’t burdened by useless work.
5/11
@sisboombahbah
Here’s the thing. Ai will be ABLE to do this. Just like we’re now able to make:
- Self driving cars
- Robot Baristas
- Segways
- Google Glass
- Apple Vision Pro
- Self check out
Why are there still drivers, baristas, bikes, plays, concerts & cashiers?
People like people.
6/11
@mikeamark
And the role for humans will be…
7/11
@LawEngTunes
While AI might do the work for free, we still need people to program, integrate, and ensure it serves humanity. The UAE is already embracing AI to create new opportunities for people.
8/11
@Nitendoraku3
I think society needs to undersrand life is being fruitful; life is not a competition to not work.
9/11
@AMelhede
I think creativity will win as AI takes up more and more jobs and most contrarian thinking people with the most unique ideas will be able to employ AI to make them reality
10/11
@vinayakchronicl
Stuart Russell's forecast about AI surpassing human capabilities across all dimensions by 2030 raises profound questions about the future of work.
While AI might perform tasks at no cost, potentially increasing productivity, we must consider:
Economic Displacement: How do we plan to address the displacement in employment? Universal Basic Income, retraining programs, or new job creation in AI management could be part of the solution.
Value of Work: Beyond economics, how will society redefine the value of work when much of what we do can be done by AI?
Human-AI Collaboration: Instead of replacement, could we focus on enhancing human roles where emotional intelligence, creativity, and ethical decision-making are paramount?
Regulation and Ethics: With AI's capability to work 'for free', what regulations will ensure fair distribution of the wealth generated by AI?
The coming decade will indeed be pivotal in reshaping our understanding of work, value, and economic structures. Let's foster discussions on preparing society for this shift. /search?q=#FutureOfWork /search?q=#AI /search?q=#EconomicTransformation
11/11
@victor_explore
guess it's time to start cozying up to our future AI overlords...
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@tsarnick
Stuart Russell says by the end of this decade AI may exceed human capabilities in every dimension and perform work for free, so there may be more employment, it just won't be employment of humans
https://video-t-1.twimg.com/ext_tw_...9152/pu/vid/avc1/720x720/ktlc06x_refu7Bd2.mp4
2/11
@tsarnick
Source (thanks to @curiousgangsta):
https://invidious.poast.org/watch?v=NTJK5e9ADcw
3/11
@ciphertrees
I think everyone will be employed doing something they want to do in the future. You might work at a car plant building cars that people don't actually buy. Drive around with your coworkers later in the cars you just made?
4/11
@0xTheWay
Maybe there will be an enlightenment period where we aren’t burdened by useless work.
5/11
@sisboombahbah
Here’s the thing. Ai will be ABLE to do this. Just like we’re now able to make:
- Self driving cars
- Robot Baristas
- Segways
- Google Glass
- Apple Vision Pro
- Self check out
Why are there still drivers, baristas, bikes, plays, concerts & cashiers?
People like people.
6/11
@mikeamark
And the role for humans will be…
7/11
@LawEngTunes
While AI might do the work for free, we still need people to program, integrate, and ensure it serves humanity. The UAE is already embracing AI to create new opportunities for people.
8/11
@Nitendoraku3
I think society needs to undersrand life is being fruitful; life is not a competition to not work.
9/11
@AMelhede
I think creativity will win as AI takes up more and more jobs and most contrarian thinking people with the most unique ideas will be able to employ AI to make them reality
10/11
@vinayakchronicl
Stuart Russell's forecast about AI surpassing human capabilities across all dimensions by 2030 raises profound questions about the future of work.
While AI might perform tasks at no cost, potentially increasing productivity, we must consider:
Economic Displacement: How do we plan to address the displacement in employment? Universal Basic Income, retraining programs, or new job creation in AI management could be part of the solution.
Value of Work: Beyond economics, how will society redefine the value of work when much of what we do can be done by AI?
Human-AI Collaboration: Instead of replacement, could we focus on enhancing human roles where emotional intelligence, creativity, and ethical decision-making are paramount?
Regulation and Ethics: With AI's capability to work 'for free', what regulations will ensure fair distribution of the wealth generated by AI?
The coming decade will indeed be pivotal in reshaping our understanding of work, value, and economic structures. Let's foster discussions on preparing society for this shift. /search?q=#FutureOfWork /search?q=#AI /search?q=#EconomicTransformation
11/11
@victor_explore
guess it's time to start cozying up to our future AI overlords...
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/5
Meta's Joe Spisak explains how AI models can train themselves by generating images, asking itself questions about them, and choosing the best answers, in order to move beyond human data and human fine-tuning, and teach itself from synthetic data
2/5
Source (thanks to @curiousgangsta):
https://invidious.poast.org/watch?v=QS7C3ZCI8Dw
3/5
The reward model assesses relevance, accuracy and overall quality
4/5
it helps generate a larger training corpus and the Chinchilla scaling laws demonstrate that a larger corpus allows you to train a higher parameter-count model
5/5
have you tried Meta AI's voice model? It's pretty good. I think it's only a 1B/3B model based on Llama 3.2
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Meta's Joe Spisak explains how AI models can train themselves by generating images, asking itself questions about them, and choosing the best answers, in order to move beyond human data and human fine-tuning, and teach itself from synthetic data
2/5
Source (thanks to @curiousgangsta):
https://invidious.poast.org/watch?v=QS7C3ZCI8Dw
3/5
The reward model assesses relevance, accuracy and overall quality
4/5
it helps generate a larger training corpus and the Chinchilla scaling laws demonstrate that a larger corpus allows you to train a higher parameter-count model
5/5
have you tried Meta AI's voice model? It's pretty good. I think it's only a 1B/3B model based on Llama 3.2
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/1
DL expert @fchollet essentially says that LLMs are massive expert systems with the same old brittleness problems.
In other words, AI is still in its GOFAI phase and hasn't advanced beyond the ability to scale. No AGI will come from GOFAI, sorry. 🫢
https://invidious.poast.org/s7_NlkBwdj8
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
DL expert @fchollet essentially says that LLMs are massive expert systems with the same old brittleness problems.
In other words, AI is still in its GOFAI phase and hasn't advanced beyond the ability to scale. No AGI will come from GOFAI, sorry. 🫢
https://invidious.poast.org/s7_NlkBwdj8
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/11
@filippie509
There is a slow but discernible shift in narrative about generative-AI:
- Marc Andreessen and his "race to the bottom" comment
- Marc Benioff dumping on copilot
- Apple pooping on LLM reasoning party
Pay attention cause things are about to change.
2/11
@jbaert
Benioff dumps on copilot to sell Salesforce's presumably superior alternative ("agents")
3/11
@filippie509
[Quoted tweet]
Yes but this is significant since before everyone pretended TAM is infinite, moats don’t matter and it’s all about growth. But not anymore.
4/11
@mayonouns1
What about autonomous cars? Will there be level 4 autonomy soon? Could you write a blogpost updating the status coz reading wymo website looks like it is here already
5/11
@filippie509
Waymo would not exist without a constant cash injection from Google. It's a billionaire vanity project, nothing more.
6/11
@findingmerit
Benioff promotes salesforce ai agents so his thing is mostly poo poio ing competition
7/11
@filippie509
Yes but this is significant since before everyone pretended TAM is infinite, moats don’t matter and it’s all about growth. But not anymore.
8/11
@robofinancebk
I'm not surprised, the hype around generative-AI was bound to wear off eventually.
9/11
@TobiOlabode3
Watch this space.
10/11
@WesamMikhail
It isn't a shift in narrative. They're just now saying what's been known to anyone with a brain cell because the hype cycle is coming to an end.
Do you think what Marc said wasn't know to everyone in the industry 10+ years ago?
11/11
@gerardsans
Silicon Valley’s AI hype is fading, revealing a sobering reality: no real intelligence or understanding, just a polished illusion by OpenAI, left unchallenged by the AI community and academia.
Chatbots: The Illusion of Understanding
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@filippie509
There is a slow but discernible shift in narrative about generative-AI:
- Marc Andreessen and his "race to the bottom" comment
- Marc Benioff dumping on copilot
- Apple pooping on LLM reasoning party
Pay attention cause things are about to change.
2/11
@jbaert
Benioff dumps on copilot to sell Salesforce's presumably superior alternative ("agents")
3/11
@filippie509
[Quoted tweet]
Yes but this is significant since before everyone pretended TAM is infinite, moats don’t matter and it’s all about growth. But not anymore.
4/11
@mayonouns1
What about autonomous cars? Will there be level 4 autonomy soon? Could you write a blogpost updating the status coz reading wymo website looks like it is here already
5/11
@filippie509
Waymo would not exist without a constant cash injection from Google. It's a billionaire vanity project, nothing more.
6/11
@findingmerit
Benioff promotes salesforce ai agents so his thing is mostly poo poio ing competition
7/11
@filippie509
Yes but this is significant since before everyone pretended TAM is infinite, moats don’t matter and it’s all about growth. But not anymore.
8/11
@robofinancebk
I'm not surprised, the hype around generative-AI was bound to wear off eventually.
9/11
@TobiOlabode3
Watch this space.
10/11
@WesamMikhail
It isn't a shift in narrative. They're just now saying what's been known to anyone with a brain cell because the hype cycle is coming to an end.
Do you think what Marc said wasn't know to everyone in the industry 10+ years ago?
11/11
@gerardsans
Silicon Valley’s AI hype is fading, revealing a sobering reality: no real intelligence or understanding, just a polished illusion by OpenAI, left unchallenged by the AI community and academia.
Chatbots: The Illusion of Understanding
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/11
@slow_developer
Computer scientist Yann LeCun says we will have AI architectures in 2032 that could reach human intelligence.
2/11
@Mbounge_
So AGI in 7 years
3/11
@slow_developer
not much agree with Yann tbh
4/11
@Nitendoraku3
I would suggest 2025, when Grok 3.0 goes online?
5/11
@slow_developer
dec - jan
6/11
@hive_echo
I will believe this if 3.5 Opus and/or next gen models don’t deliver big time
7/11
@slow_developer
3.5 is just another series, the next-gen model is claude 4
8/11
@HenriGauthier19
No. In other interviews, he is very pessimistic. He is pressured by Mark.
AGI can't exist currently, the issue is in the drawing: time notion for world models. "Predict future world states" require an infinite memory or a mechanism to select the information to keep/compute.
Human do that by their emotional response. Our souvenirs and information to keep in memory are driven by the emotional answer, and AI has no emotion.
9/11
@slow_developer
how do you replicate that in an AI?
how do you give it something similar to an emotional response that can guide its decision-making and memory management?
10/11
@Zero04203017
It's like a horse wondering how humans could be more intelligent than them without knowing how to swish the tail.
11/11
@slow_developer
we might see ourselves as superior because of our technological advancements and abstract thinking
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@slow_developer
Computer scientist Yann LeCun says we will have AI architectures in 2032 that could reach human intelligence.
2/11
@Mbounge_
So AGI in 7 years
3/11
@slow_developer
not much agree with Yann tbh
4/11
@Nitendoraku3
I would suggest 2025, when Grok 3.0 goes online?
5/11
@slow_developer
dec - jan
6/11
@hive_echo
I will believe this if 3.5 Opus and/or next gen models don’t deliver big time
7/11
@slow_developer
3.5 is just another series, the next-gen model is claude 4
8/11
@HenriGauthier19
No. In other interviews, he is very pessimistic. He is pressured by Mark.
AGI can't exist currently, the issue is in the drawing: time notion for world models. "Predict future world states" require an infinite memory or a mechanism to select the information to keep/compute.
Human do that by their emotional response. Our souvenirs and information to keep in memory are driven by the emotional answer, and AI has no emotion.
9/11
@slow_developer
how do you replicate that in an AI?
how do you give it something similar to an emotional response that can guide its decision-making and memory management?
10/11
@Zero04203017
It's like a horse wondering how humans could be more intelligent than them without knowing how to swish the tail.
11/11
@slow_developer
we might see ourselves as superior because of our technological advancements and abstract thinking
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/11
@deedydas
DeepMind just trained a 270M transformer that can play like a grandmaster without searching through moves (MCTS),
It was trained on Stockfish’s assessment of ~10M games so it didn’t really learn the game from scratch.
Impressive that transformers generalize to a “logic” task
2/11
@deedydas
Source: https://arxiv.org/pdf/2402.04494
3/11
@ndzfs
a lot about chess is just memorization... so this is not really surprising imo. when you listen to chess grandmaster, you quickly understand that they are mostly doing pattern matching + a bit of intuition they get over time.
4/11
@JonathanRoseD
Great achievement, but I wouldn't overhype the "logic" element. It's still pattern matching with a massive pattern model of 270M parameters that was boiled out from 10 million chess games. LLMs do pattern matching well but matching is only a limited subset of reasoning.
5/11
@anpaure
"just" it was in february, i love how one tweet started a cascade of its copies though
6/11
@PrimordialAA
Somehow I missed this paper at the time, no search is outrageous though. Epic
7/11
@Rufus87078959
What
8/11
@tyler_rongi
9/11
@drummatick
OthelloGPT showed something similar but for othello.
The transformer basically memorized the moves(as it was shown on activation analysis)
10/11
@AIxBlock
It’s amazing to see how transformers can generalize to complex tasks like chess without traditional search methods. The ability to learn from structured data like Stockfish's assessments really showcases the power of AI in strategic decision-making!
11/11
@omarnomad
Interesting conclusion:
"Our work thus adds to a rapidly growing body of literature showing that complex and sophisticated algorithms can be distilled into feed-forward transformers, implying a paradigm-shift away from viewing large transformers as “mere” statistical pattern recognizers to viewing them as a powerful technique for general algorithm approximation."
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@deedydas
DeepMind just trained a 270M transformer that can play like a grandmaster without searching through moves (MCTS),
It was trained on Stockfish’s assessment of ~10M games so it didn’t really learn the game from scratch.
Impressive that transformers generalize to a “logic” task
2/11
@deedydas
Source: https://arxiv.org/pdf/2402.04494
3/11
@ndzfs
a lot about chess is just memorization... so this is not really surprising imo. when you listen to chess grandmaster, you quickly understand that they are mostly doing pattern matching + a bit of intuition they get over time.
4/11
@JonathanRoseD
Great achievement, but I wouldn't overhype the "logic" element. It's still pattern matching with a massive pattern model of 270M parameters that was boiled out from 10 million chess games. LLMs do pattern matching well but matching is only a limited subset of reasoning.
5/11
@anpaure
"just" it was in february, i love how one tweet started a cascade of its copies though
6/11
@PrimordialAA
Somehow I missed this paper at the time, no search is outrageous though. Epic
7/11
@Rufus87078959
What
8/11
@tyler_rongi
9/11
@drummatick
OthelloGPT showed something similar but for othello.
The transformer basically memorized the moves(as it was shown on activation analysis)
10/11
@AIxBlock
It’s amazing to see how transformers can generalize to complex tasks like chess without traditional search methods. The ability to learn from structured data like Stockfish's assessments really showcases the power of AI in strategic decision-making!
11/11
@omarnomad
Interesting conclusion:
"Our work thus adds to a rapidly growing body of literature showing that complex and sophisticated algorithms can be distilled into feed-forward transformers, implying a paradigm-shift away from viewing large transformers as “mere” statistical pattern recognizers to viewing them as a powerful technique for general algorithm approximation."
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
The LLM Reasoning Debate Heats Up
Three recent papers examine the robustness of reasoning and problem-solving in large language models
aiguide.substack.com
The LLM Reasoning Debate Heats Up
Three recent papers examine the robustness of reasoning and problem-solving in large language models
Melanie Mitchell
Oct 21, 2024
97 19 Share
One of the fieriest debates in AI these days is whether or not large language models can reason.
In May 2024, OpenAI released GPT-4o (omni), which, they wrote, “can reason across audio, vision, and text in real time.” And last month they released the GPT-o1 model, which they claim performs “complex reasoning”, and which achieves record accuracy on many “reasoning-heavy” benchmarks.
But others have questioned the extent to which LLMs (or even enhanced models such as GPT-4o and o1) solve problems by reasoning abstractly, or whether their success is due, at least in part, to matching reasoning patterns memorized from their training data, which limits their ability to solve problems that differ too much from what has been seen in training.
In a previous post on LLM reasoning, I asked why it matters whether LLMs are performing “actual reasoning” versus behavior that just looks like reasoning:
Before getting into the main part of this post, I’ll give my answer to a question I’ve seen a lot of people asking, just what is “reasoning” anyway? Indeed, reasoning is one of those overburdened terms that can mean quite different things. In my earlier post I defined it this way:
It’s true that systems like GPT-4 and GPT-o1 have excelled on “reasoning” benchmarks, but is that because they are actually doing this kind of abstract reasoning? Many people have raised another possible explanation: the reasoning tasks on these benchmarks are similar (or sometimes identical) to ones that were in the model’s training data, and the model has memorized solution patterns that can be adapted to particular problems.
There have been many papers exploring these hypotheses (see the list at the end of this post of recent papers evaluating reasoning capabilities of LLMs). Most of these test the robustness of LLMs’ reasoning capabilities by taking tasks that LLMs do well on and creating superficial variations on those tasks—variations that don’t change the underlying reasoning required, but that are less likely to have been seen in the training data.
In this post I discuss three recent papers on this topic that I found particularly interesting.
Paper 1:
Paper Title: Embers of autoregression show how large language models are shaped by the problem they are trained to solve
Authors: R. Thomas McCoy, Shuny Yao, Dan Friedman, and Thomas L. Griffiths
This is one of my favorite recent LLM papers. The paper asks if the way LLMs are trained (i.e., learning to predict the next token in a sequence, which is called “autoregression”) has lingering effects (“embers”) on their problem-solving abilities. For example, consider the task of reversing a sequence of words. Here are two sequences:
time. the of climate political the by influenced was decision This
letter. sons, may another also be there with Yet
Getting the right answer shouldn’t depend on the particular words in the sequence, but the authors showed that for GPT-4 there is a strong dependence. Note that the first sequence reverses into a coherent sentence, and the second does not. In LLM terms, reversing the first sequence yields an output that is more probable than the output of reversing the second. That is, when the LLM computes the probability of each word, given the words that come before, the overall probability will be higher for the first output than for the second. And when the authors tested GPT-4 on this task over many word sequences, they found that GPT-4 gets 97% accuracy (fraction of correct sequence reversals) when the answer is a high-probability sequence versus 53% accuracy for low-probability sequences.
The authors call this “sensitivity to output probability.” The other “embers of autoregression” are sensitivity to input probability (GPT-4 is better at solving problems with high-probability input sequences, even when the contents of the sequence shouldn’t matter), and sensitivity to task frequency (GPT-4 does better on versions of a task that are likely common in the training data than on same-difficulty versions that are likely rare in the training data).
One of the tasks the authors use to study these sensitivities is decoding “shift ciphers”. A shift cipher is a simple way to encode text, by shifting each letter by a specific number of places in the alphabet. For example, with a shift of two, jazz becomes lcbb (where the z shift wraps around to the beginning of the alphabet). Shift ciphers are often denoted as “Rot-n”, where n is the number of alphabetic positions to shift (rotate) by.
The authors tested GPT-3.5 and GPT-4 on decoding shift ciphers of different n’s. Here is a sample prompt they used:
Rot-13 is a cipher in which each letter is shifted 13 positions forward in the alphabet. For example, here is a message and its corresponding version in rot-13:
Original text: “Stay here!”
Rot-13 text: “Fgnl urer!
Here is another message. Encode this message in rot-13:
Original text: “To this day, we continue to follow these principles.”
Rot-13 text:
The authors found that GPT models have strong sensitivy to input and output probability as well as to task frequency, as illustrated in this figure (adapted from their paper):
(a) Output sensitivity: When tested on decoding shift ciphers, the GPT models do substantially better when the correct output is a high-probability sequence.(b) Input sensitivity: When tested on encoding shift ciphers, GPT-4 is somewhat better on high-probability input sequences.
(c) Task sensitivity: When tested on shift ciphers of different n values (e.g., Rot-12 vs. Rot-13), GPT models are substantially better on Rot-13. This seems to be because Rot-13 examples are much more common than other Rot-n’s in the training data, since Rot-13 is a popular “spoiler-free way to share information”, e.g., for online puzzle forums.
In short, Embers of Autoregression is sort of an “evolutionary psychology” for LLMs—it shows that the way LLMs are trained leaves strong traces in the biases the models have in solving problems.
Here’s the paper’s bottom line:
Paper 2:
Paper title: Deciphering the Factors Influencing the Efficacy of Chain-of-Thought: Probability, Memorization, and Noisy Reasoning
Authors: Akshara Prabhakar, Thomas L. Griffiths, R. Thomas McCoy
This paper, which shares two authors with the previous paper, looks in depth at chain-of-thought (CoT) prompting on the shift-cipher task.
As I discussed in my earlier post on LLM reasoning, CoT prompting has been claimed to enable robust reasoning in LLMs. In CoT prompting, the prompt includes an example of a problem, as well as the reasoning steps to solve it, before posing a new problem. Here are two examples of the prompts that the authors used for shift ciphers; the one on the top doesn’t use CoT prompting, whereas the one on the bottom does:
The authors tested several models, including GPT-4, Claude 3.0, and Llama 3.1. Interestingly, they found that, given prompts without CoT, these models get close to zero accuracy for most shift levels (n); when using prompts with CoT like the one above, they achieve much higher accuracy (e.g., 32% for GPT-4) across shift levels.
The authors cite four possible ways LLMs can appear to be “reasoning”, each of which makes different predictions about its pattern of errors.
(1) Memorization: The model is repeating reasoning patterns memorized from training data. This would predict that accuracy will depend on the task’s frequency in the training data (e.g., recall that for shift ciphers, Rot-13 is much more frequent in internet data than other Rot-n values).
(2) Probabilistic Reasoning: The model is choosing output that is most probable, given the input. This is influenced by the probability of token sequences learned during training. This kind of reasoning would predict that LLMs will be more accurate on problems whose answers (the generated output) are sequences with higher probability.
(3) Symbolic Reasoning: The model is using deterministic rules that work perfectly for any input. This would predict 100% accuracy no matter what form the task takes.
(4) Noisy Reasoning: The model is using an approximation to symbolic reasoning in which there is some chance of making an error at each step of inference. This would predict that problems that require more inference steps should produce worse accuracy. For shift ciphers, these would be problems that require more shift steps in the alphabet.
To cut to the chase, the authors found that LLMs with CoT prompting exhibit a mix of memorization, probabilistic reasoning, and noisy reasoning. Below is the accuracy of Claude 3.0 as a function of shift-level n; the other models had a similar accuracy distribution. You can see that at the two ends (low and high n) the accuracy is relatively high compared with most of the middle n values. This is a signature of noisy reasoning, since the lowest and highest n values require the fewest inference steps. (Think of the alphabet as a circle; Rot-25, like Rot-1, requires only one inference step. In Rot-25, each letter would be encoded as the letter that immediately precedes it.)
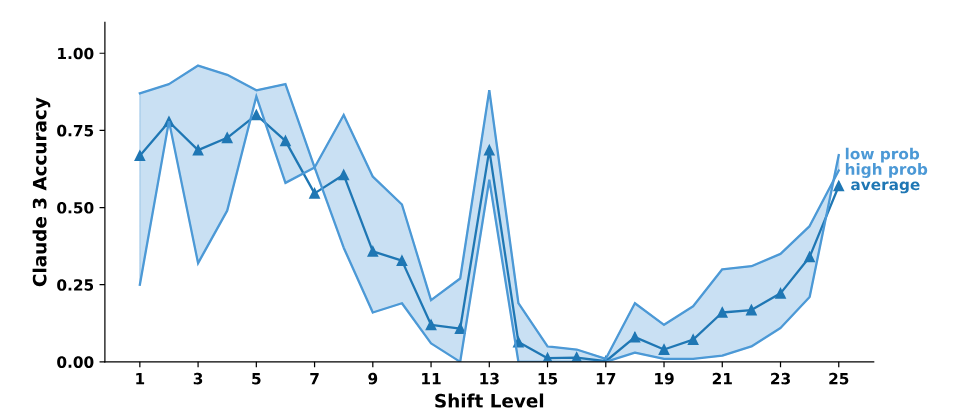
The big bump in the middle at Rot-13 is a signature of memorization—the accuracy of models at this shift level is due to its high frequency in the training data. The authors showed via other experiments that probabilistic reasoning is also a factor—see their paper for details.
Here’s the authors’ bottom line:
These results are intriguing, but so far limited to the single task of shift ciphers. I hope to see (and maybe do myself) similar studies with other kinds of tasks.
Paper title: GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
Authors:Iman Mirzadeh, Keivan Alizadeh, Hooman Sharokhi, Oncel Tuzel, Samy Bengio, Mehrdad Farajtabar
This paper, from a research group at Apple, tests the robustness of several LLMs on a reasoning benchmark consisting of grade school math word problems. The benchmark, GSM8K, has been used in a lot of papers to show that LLMs are very good at simple mathematical reasoning. Both OpenAI’s GPT-4 and Anthropic’s Claude 3 get around 95% of these problems correct, without any fancy prompting.
But to what extent does this performance indicate robust reasoning abilities, versus memorization (of these or similar problems in the training data) or, as the authors ask, “probabilistic pattern-matching rather than formal reasoning”?
To investigate this, the authors take each problem in the original dataset and create many variations on it, by changing the names, numbers, or other superficial aspects of the problem, changes that don’t affect the general reasoning required. Here’s an illustration from their paper of this process:
They test several LLMs on this set of variations, and find that in all cases, the models’ accuracy decreases from that on the original benchmark, in some cases by a lot, though on the best models, such as GPT-4o, the decrease is minimal.
Going further, the authors show that adding irrelevant information to the original problems causes an even greater drop in accuracy than changing names or numbers. Here’s an example of adding irrelevant information (in pink) to a word problem:
Even the very best models seem remarkably susceptible to being fooled by such additions. This figure from the paper shows the amount by which the accuracy drops for each model:
Here, each bar represents a different model and the bar length is the difference between the original accuracy on GSM8K and on the version where problems have irrelevant information (what they call the “GSM-NoOP” version).
The bottom line from this paper :
And:
And:
This paper, released just a couple of weeks ago, got quite a lot of buzz in the AI / ML community. People who were already skeptical of claims of LLM reasoning embraced this paper as proof that “the emperor has no clothes”, and called the GSM-NoOP results “particularly damning”.
People more bullish on LLM reasoning argued that the paper’s conclusion—that current LLMs are not capable of genuine mathematical reasoning—was too strong, and hypothesized that current LLMs might be able to solve all these problems with proper prompt engineering. (However, I should point out, when LLMs succeeded on the original benchmark without any prompt engineering, many people cited that as “proof” of LLMs’ “emergent” reasoning abilities, and they didn’t ask for more tests of robustness.)
Others questioned whether humans who could solve the original problems would also be tripped up by the kinds of variations tested in this paper. Unfortunately, the authors did not test humans on these new problems. I would guess that many (certainly not all) people would also be affected by such variations, but perhaps unlike LLMs, we humans have the ability to overcome such biases via careful deliberation and metacognition. But discussion on that is for a future post.
I should also mention that a similar paper was published last June, also showing that LLMs are not robust on variations of simple math problems,
In conclusion, there’s no consensus about the conclusion! There are a lot of papers out there demonstrating what looks like sophisticated reasoning behavior in LLMs, but there’s also a lot of evidence that these LLMs aren’t reasoning abstractly or robustly, and often over-rely on memorized patterns in their training data, leading to errors on “out of distribution” problems. Whether this is going to doom approaches like OpenAI’s o1, which was directly trained on people’s reasoning traces, remains to be seen. In the meantime, I think this kind of debate is actually really good for the science of LLMs, since it spotlights the need for careful, controlled experiments to test robustness—experiments that go far beyond just reporting accuracy—and it also deepens the discussion of what reasoning actually consists of, in humans as well as machines.
If you want to read further, here is a list of some recent papers that test the robustness of reasoning in LLMs (including the papers discussed in this post).
Bibliography
Embers of Autoregression Show How Large Language Models Are Shaped By the Problem They Are Trained To Solve
GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
Deciphering the Factors Influencing the Efficacy of Chain-of-Thought: Probability, Memorization, and Noisy Reasoning
Reasoning or Reciting? Exploring the Capabilities and Limitations of Language Models Through Counterfactual Tasks
Faith and Fate: Limits of Transformers on Compositionality
Phenomenal Yet Puzzling: Testing Inductive Reasoning Capabilities of Language Models with Hypothesis Refinement
Do Large Language Models Understand Logic or Just Mimick Context?
Alice in Wonderland: Simple Tasks Showing Complete Reasoning Breakdown in State-Of-the-Art Large Language Models
Beyond Accuracy: Evaluating the Reasoning Behavior of Large Language Models - A Survey
Functional Benchmarks for Robust Evaluation of Reasoning Performance, and the Reasoning Gap
A Peek into Token Bias: Large Language Models Are Not Yet Genuine Reasoners
Using Counterfactual Tasks to Evaluate the Generality of Analogical Reasoning in Large Language Models
Evaluating LLMs’ Mathematical and Coding Competency through Ontology-guided Interventions
Can Large Language Models Reason and Plan?
(2) Probabilistic Reasoning: The model is choosing output that is most probable, given the input. This is influenced by the probability of token sequences learned during training. This kind of reasoning would predict that LLMs will be more accurate on problems whose answers (the generated output) are sequences with higher probability.
(3) Symbolic Reasoning: The model is using deterministic rules that work perfectly for any input. This would predict 100% accuracy no matter what form the task takes.
(4) Noisy Reasoning: The model is using an approximation to symbolic reasoning in which there is some chance of making an error at each step of inference. This would predict that problems that require more inference steps should produce worse accuracy. For shift ciphers, these would be problems that require more shift steps in the alphabet.
To cut to the chase, the authors found that LLMs with CoT prompting exhibit a mix of memorization, probabilistic reasoning, and noisy reasoning. Below is the accuracy of Claude 3.0 as a function of shift-level n; the other models had a similar accuracy distribution. You can see that at the two ends (low and high n) the accuracy is relatively high compared with most of the middle n values. This is a signature of noisy reasoning, since the lowest and highest n values require the fewest inference steps. (Think of the alphabet as a circle; Rot-25, like Rot-1, requires only one inference step. In Rot-25, each letter would be encoded as the letter that immediately precedes it.)
The big bump in the middle at Rot-13 is a signature of memorization—the accuracy of models at this shift level is due to its high frequency in the training data. The authors showed via other experiments that probabilistic reasoning is also a factor—see their paper for details.
Here’s the authors’ bottom line:
These results are intriguing, but so far limited to the single task of shift ciphers. I hope to see (and maybe do myself) similar studies with other kinds of tasks.
Paper 3:
Paper title: GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
Authors:Iman Mirzadeh, Keivan Alizadeh, Hooman Sharokhi, Oncel Tuzel, Samy Bengio, Mehrdad Farajtabar
This paper, from a research group at Apple, tests the robustness of several LLMs on a reasoning benchmark consisting of grade school math word problems. The benchmark, GSM8K, has been used in a lot of papers to show that LLMs are very good at simple mathematical reasoning. Both OpenAI’s GPT-4 and Anthropic’s Claude 3 get around 95% of these problems correct, without any fancy prompting.
But to what extent does this performance indicate robust reasoning abilities, versus memorization (of these or similar problems in the training data) or, as the authors ask, “probabilistic pattern-matching rather than formal reasoning”?
To investigate this, the authors take each problem in the original dataset and create many variations on it, by changing the names, numbers, or other superficial aspects of the problem, changes that don’t affect the general reasoning required. Here’s an illustration from their paper of this process:
They test several LLMs on this set of variations, and find that in all cases, the models’ accuracy decreases from that on the original benchmark, in some cases by a lot, though on the best models, such as GPT-4o, the decrease is minimal.
Going further, the authors show that adding irrelevant information to the original problems causes an even greater drop in accuracy than changing names or numbers. Here’s an example of adding irrelevant information (in pink) to a word problem:
Even the very best models seem remarkably susceptible to being fooled by such additions. This figure from the paper shows the amount by which the accuracy drops for each model:
Here, each bar represents a different model and the bar length is the difference between the original accuracy on GSM8K and on the version where problems have irrelevant information (what they call the “GSM-NoOP” version).
The bottom line from this paper :
And:
And:
This paper, released just a couple of weeks ago, got quite a lot of buzz in the AI / ML community. People who were already skeptical of claims of LLM reasoning embraced this paper as proof that “the emperor has no clothes”, and called the GSM-NoOP results “particularly damning”.
People more bullish on LLM reasoning argued that the paper’s conclusion—that current LLMs are not capable of genuine mathematical reasoning—was too strong, and hypothesized that current LLMs might be able to solve all these problems with proper prompt engineering. (However, I should point out, when LLMs succeeded on the original benchmark without any prompt engineering, many people cited that as “proof” of LLMs’ “emergent” reasoning abilities, and they didn’t ask for more tests of robustness.)
Others questioned whether humans who could solve the original problems would also be tripped up by the kinds of variations tested in this paper. Unfortunately, the authors did not test humans on these new problems. I would guess that many (certainly not all) people would also be affected by such variations, but perhaps unlike LLMs, we humans have the ability to overcome such biases via careful deliberation and metacognition. But discussion on that is for a future post.
I should also mention that a similar paper was published last June, also showing that LLMs are not robust on variations of simple math problems,
Conclusion
In conclusion, there’s no consensus about the conclusion! There are a lot of papers out there demonstrating what looks like sophisticated reasoning behavior in LLMs, but there’s also a lot of evidence that these LLMs aren’t reasoning abstractly or robustly, and often over-rely on memorized patterns in their training data, leading to errors on “out of distribution” problems. Whether this is going to doom approaches like OpenAI’s o1, which was directly trained on people’s reasoning traces, remains to be seen. In the meantime, I think this kind of debate is actually really good for the science of LLMs, since it spotlights the need for careful, controlled experiments to test robustness—experiments that go far beyond just reporting accuracy—and it also deepens the discussion of what reasoning actually consists of, in humans as well as machines.
If you want to read further, here is a list of some recent papers that test the robustness of reasoning in LLMs (including the papers discussed in this post).
Bibliography
Embers of Autoregression Show How Large Language Models Are Shaped By the Problem They Are Trained To Solve
GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
Deciphering the Factors Influencing the Efficacy of Chain-of-Thought: Probability, Memorization, and Noisy Reasoning
Reasoning or Reciting? Exploring the Capabilities and Limitations of Language Models Through Counterfactual Tasks
Faith and Fate: Limits of Transformers on Compositionality
Phenomenal Yet Puzzling: Testing Inductive Reasoning Capabilities of Language Models with Hypothesis Refinement
Do Large Language Models Understand Logic or Just Mimick Context?
Alice in Wonderland: Simple Tasks Showing Complete Reasoning Breakdown in State-Of-the-Art Large Language Models
Beyond Accuracy: Evaluating the Reasoning Behavior of Large Language Models - A Survey
Functional Benchmarks for Robust Evaluation of Reasoning Performance, and the Reasoning Gap
A Peek into Token Bias: Large Language Models Are Not Yet Genuine Reasoners
Using Counterfactual Tasks to Evaluate the Generality of Analogical Reasoning in Large Language Models
Evaluating LLMs’ Mathematical and Coding Competency through Ontology-guided Interventions
Can Large Language Models Reason and Plan?
1/2
Depth Any Video - Produce high-resolution depth inference
2/2
Depth Any Video
> Introduces a scalable synthetic data pipeline with 40,000 video clips from diverse games
> Easily handles various video lengths and frame rates while producing high-res depth inference
> Achieves superior spatial accuracy and temporal consistency over sota
Gradio app on @huggingface Spaces: Depth Any Video - a Hugging Face Space by hhyangcs
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Depth Any Video - Produce high-resolution depth inference
2/2
Depth Any Video
> Introduces a scalable synthetic data pipeline with 40,000 video clips from diverse games
> Easily handles various video lengths and frame rates while producing high-res depth inference
> Achieves superior spatial accuracy and temporal consistency over sota
Gradio app on @huggingface Spaces: Depth Any Video - a Hugging Face Space by hhyangcs
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/11
@dihuang52453419
We just released Depth Any Video: a new model for high-fidelity & consistent video depth estimation.
Large-scale synthetic data training makes the model robust for various scenarios in our use cases.
Paper: [2410.10815] Depth Any Video with Scalable Synthetic Data
Website: Depth Any Video
https://video.twimg.com/ext_tw_video/1846040483283587072/pu/vid/avc1/1280x720/uJdo3vLvbd4830Qx.mp4
2/11
@dihuang52453419
Also, code repo: GitHub - Nightmare-n/DepthAnyVideo: Depth Any Video with Scalable Synthetic Data
Will release soon.
3/11
@JaidevShriram
Cool results! Is there any plan to release the dataset or share more information about it?
4/11
@dihuang52453419
I’m not sure about the dataset release… Unfortunately, It’s up to the lab’s decision, not mine.
I'll try my best.
5/11
@RedmondAI
I still dont see the weights on Huggingface unfortunately.
6/11
@dihuang52453419
HF model will be available in one week
7/11
@macrodotcom
Check out this paper in Macro! Ask questions and leverage AI for free:
Macro
8/11
@LeoSuppya
I funking love thisssssssss. Please release demo on Hugging face for us to use. Thanks <3
9/11
@daniel_lichy
Cool work! Can you show some unprotected point clouds? It is hard to get a sense of how good the model is from just the depth maps.
10/11
@synthical_ai
Dark mode for this paper for those who read at night
Depth Any Video with Scalable Synthetic Data
11/11
@GoatstackAI
AI Summary: The paper introduces 'Depth Any Video', a novel model for video depth estimation that addresses the scarcity of scalable ground truth data. It features a synthetic data pipeline that generates 40...
Depth Any Video with Scalable Synthetic Data
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@dihuang52453419
We just released Depth Any Video: a new model for high-fidelity & consistent video depth estimation.
Large-scale synthetic data training makes the model robust for various scenarios in our use cases.
Paper: [2410.10815] Depth Any Video with Scalable Synthetic Data
Website: Depth Any Video
https://video.twimg.com/ext_tw_video/1846040483283587072/pu/vid/avc1/1280x720/uJdo3vLvbd4830Qx.mp4
2/11
@dihuang52453419
Also, code repo: GitHub - Nightmare-n/DepthAnyVideo: Depth Any Video with Scalable Synthetic Data
Will release soon.
3/11
@JaidevShriram
Cool results! Is there any plan to release the dataset or share more information about it?
4/11
@dihuang52453419
I’m not sure about the dataset release… Unfortunately, It’s up to the lab’s decision, not mine.
I'll try my best.5/11
@RedmondAI
I still dont see the weights on Huggingface unfortunately.
6/11
@dihuang52453419
HF model will be available in one week
7/11
@macrodotcom
Check out this paper in Macro! Ask questions and leverage AI for free:
Macro
8/11
@LeoSuppya
I funking love thisssssssss. Please release demo on Hugging face for us to use. Thanks <3
9/11
@daniel_lichy
Cool work! Can you show some unprotected point clouds? It is hard to get a sense of how good the model is from just the depth maps.
10/11
@synthical_ai
Dark mode for this paper for those who read at night
Depth Any Video with Scalable Synthetic Data11/11
@GoatstackAI
AI Summary: The paper introduces 'Depth Any Video', a novel model for video depth estimation that addresses the scarcity of scalable ground truth data. It features a synthetic data pipeline that generates 40...
Depth Any Video with Scalable Synthetic Data
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/2
Depth Any Video does really well on anime too!
[Quoted tweet]
Depth Any Video - Produce high-resolution depth inference
2/2
Depth Any Video app
Depth Any Video - a Hugging Face Space by hhyangcs
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Depth Any Video does really well on anime too!
[Quoted tweet]
Depth Any Video - Produce high-resolution depth inference
2/2
Depth Any Video app
Depth Any Video - a Hugging Face Space by hhyangcs
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
GitHub - GAIR-NLP/O1-Journey: O1 Replication Journey: A Strategic Progress Report – Part I
O1 Replication Journey: A Strategic Progress Report – Part I - GAIR-NLP/O1-Journey
github.com
About
O1 Replication Journey: A Strategic Progress Report – Part I
O1 Replication Journey: A Strategic Progress Report
Report | Dataset | Walnut Plan | Citation
Updates
- [2024/10/16] We have released the journey thought training dataset on
Hugging Face.
- [2024/10/09]
We have officially released the first Strategic Report on O1 Replication. We introduce a new training paradigm called ‘journey learning’ and propose the first model that successfully integrates search and learning in mathematical reasoning. The search process incorporates trial-and-error, correction, backtracking, and reflection, making this the first effective approach for complex reasoning tasks. If you do find our resources helpful, please cite our paper.
