[Submitted on 11 Jun 2024 (v1), last revised 13 Jun 2024 (this version, v2)]
Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B
Di Zhang, Xiaoshui Huang, Dongzhan Zhou, Yuqiang Li, Wanli Ouyang| Subjects: | Artificial Intelligence (cs.AI) |
| Cite as: | arXiv:2406.07394 [cs.AI] |
| (or arXiv:2406.07394v2 [cs.AI] for this version) | |
| [2406.07394] Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B |
Submission history
From: Di Zhang [view email][v1] Tue, 11 Jun 2024 16:01:07 UTC (106 KB)
[v2] Thu, 13 Jun 2024 07:19:06 UTC (106 KB)
1/1
Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B: A Technical Report
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B: A Technical Report
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/6
It's finally here. Q* rings true. Tiny LLMs are as good at math as a frontier model.
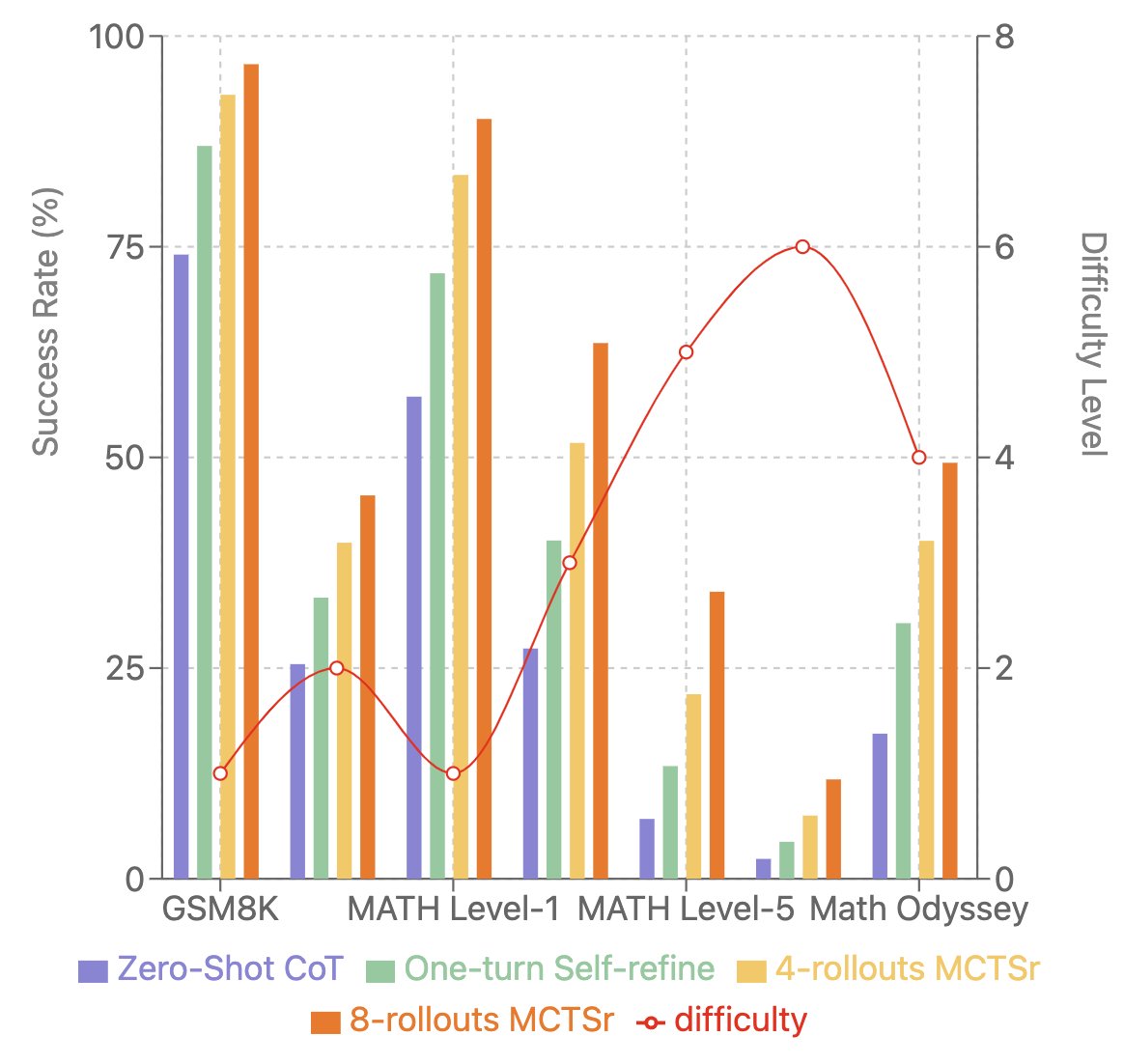
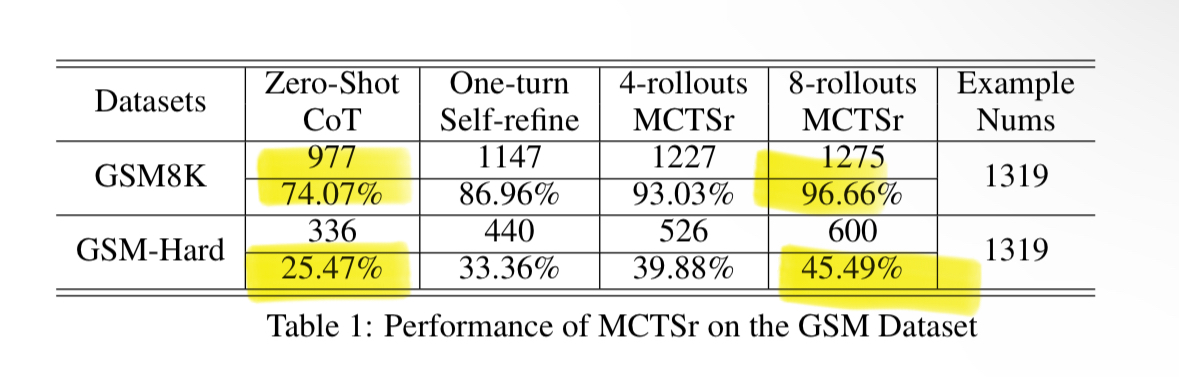
By using the same techniques Google used to solve Go (MTCS and backprop), Llama8B gets 96.7% on math benchmark GSM8K!
That’s better than GPT-4, Claude and Gemini, with 200x less parameters!
2/6
Source: https://arxiv.org/pdf/2406.07394
3/6
I'd imagine these are the techniques code foundational model trainers are using, but I wonder
a) you're limited by the ability of the base open source model and might get it to be as good as a frontier model, but barely.
b) whether you can generate enough volume of synthetic code data with reasonable $$ spend.
c) If you are doing this on a 1T+ param model, can be prohibitively expensive
4/6
The (purported) technique isn’t tied to a particular model
5/6
Come on it's SLIGHTLY harder than that
6/6
Shanghai AI lab made rumored Q* reality
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
It's finally here. Q* rings true. Tiny LLMs are as good at math as a frontier model.
By using the same techniques Google used to solve Go (MTCS and backprop), Llama8B gets 96.7% on math benchmark GSM8K!
That’s better than GPT-4, Claude and Gemini, with 200x less parameters!
2/6
Source: https://arxiv.org/pdf/2406.07394
3/6
I'd imagine these are the techniques code foundational model trainers are using, but I wonder
a) you're limited by the ability of the base open source model and might get it to be as good as a frontier model, but barely.
b) whether you can generate enough volume of synthetic code data with reasonable $$ spend.
c) If you are doing this on a 1T+ param model, can be prohibitively expensive
4/6
The (purported) technique isn’t tied to a particular model
5/6
Come on it's SLIGHTLY harder than that
6/6
Shanghai AI lab made rumored Q* reality
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/1
A prompt-level formula to add Search to LLM
Read of the day, day 85: Accessing GPT-4 level Mathematical Olympiad Solutions Via Monte Carlo Tree Self-refine with Llama-3 8B: A technical report, by Zhang et al from Shanghai Artificial Intelligence Laboratory
https://arxiv.org/pdf/2406.07394
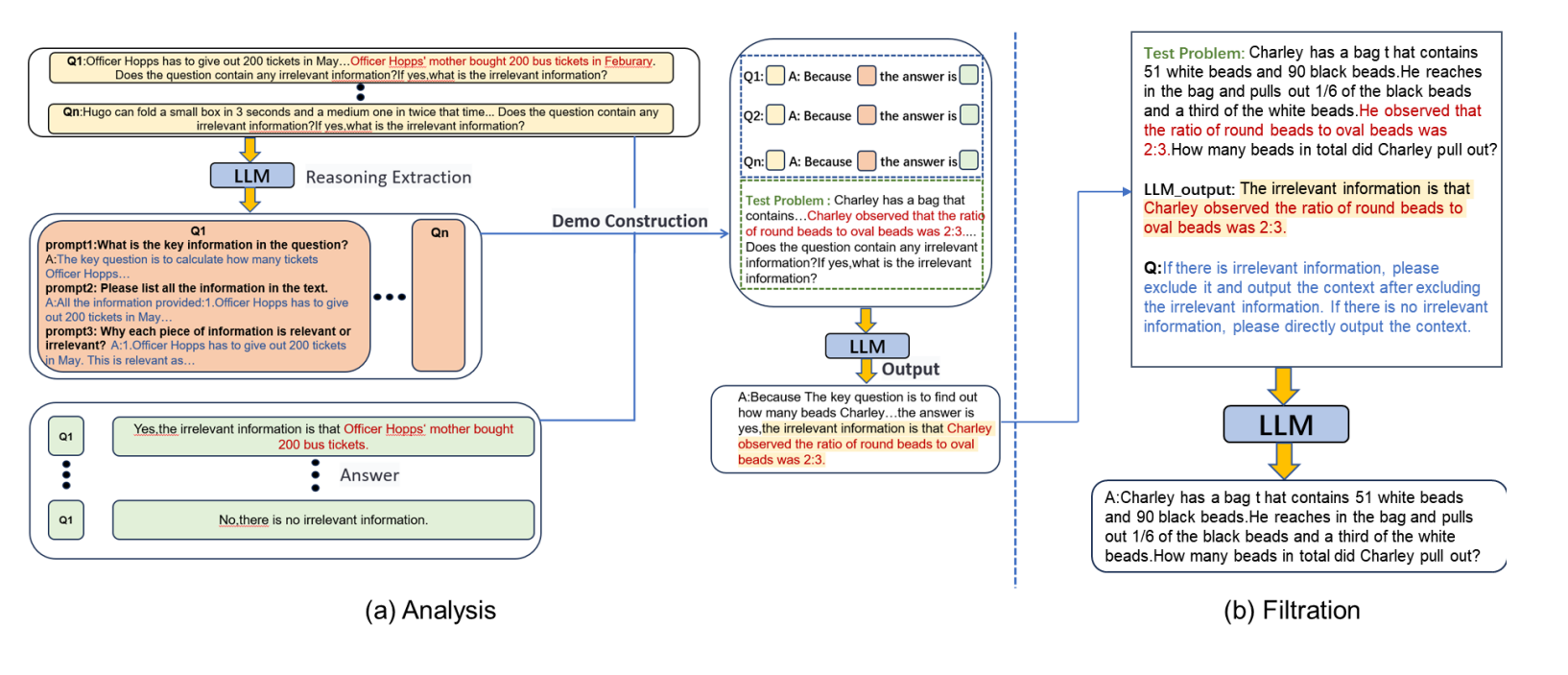
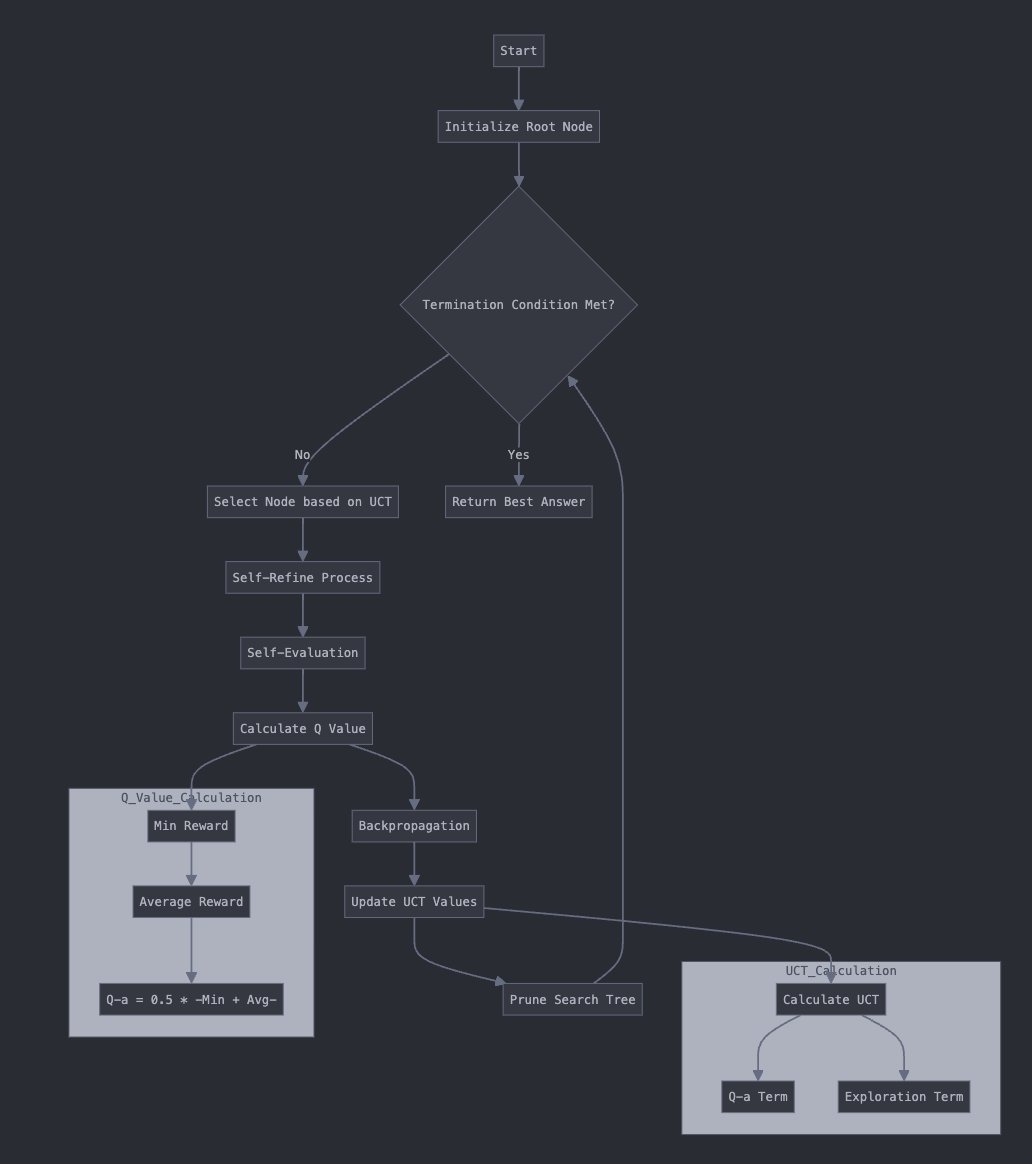
The authors of this paper introduce a Monte-Carlo Tree Search like method to enhance model generation. They call it Monte-Carlo Tree Self-Refined, shortened as MCTSr.
Their method is based solely on prompting the model and does not modify its weight, yet greatly enhances the results.
How?
1- Generate a root node through naive answers or a dummy one
2- Use a value function Q to rank answers that were not expanded, select the best greedily
3- Optimize answer through generating a feedback, and then exploit it
4- Compute the Q value of the answer
5- Update value of parent nodes
6- Identify candidate nodes for expansion, and use UCT formula to update all nodes for iterating again
7- Iterate until max steps are reached
Value function Q is actually prompting the model to reward its answer. Model is prompted several times and its answers are averaged. Backpropagation and UCT formulas can be found within the paper.
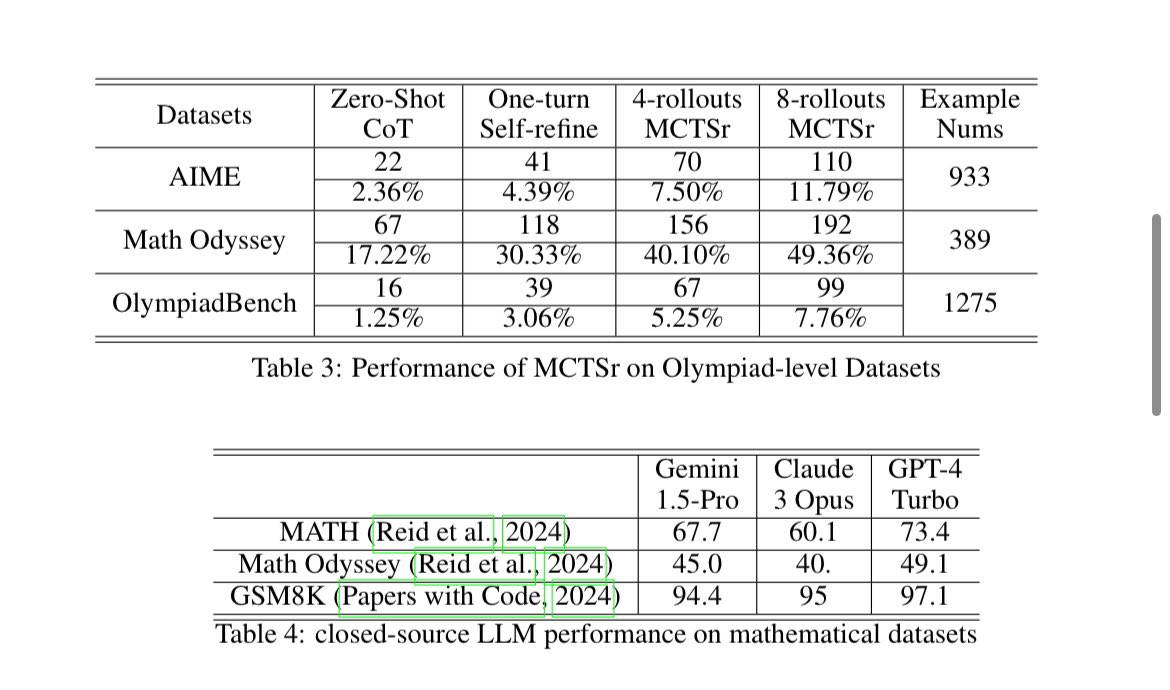
The authors then evaluate 4 rollouts and 8 rollouts MCTSr on a Llama-3 8B and compare it to GPT-4, Claude 3 Opus and Gemini-1.5 Pro on mathematical problems.
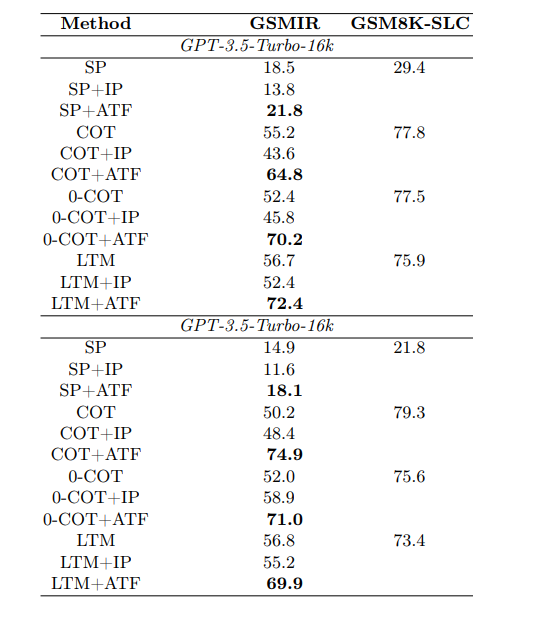
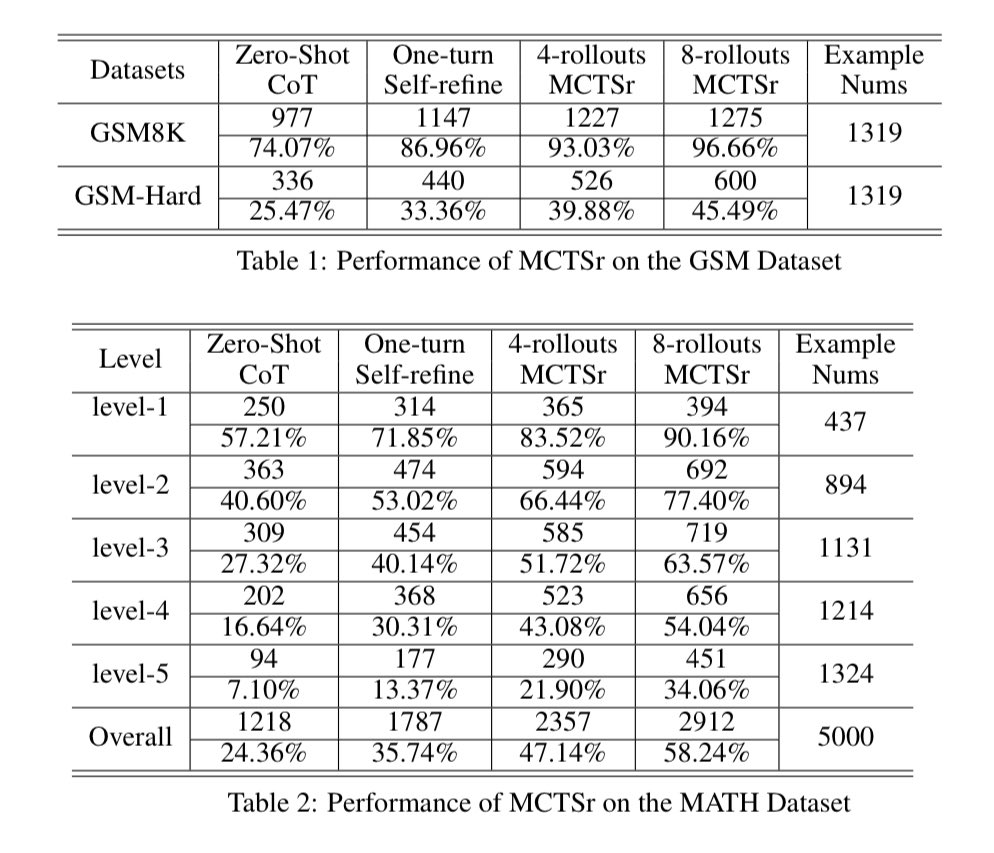
They first find out such sampling greatly increases performances on both GSM8k and MATH datasets, reaching Frontier-models level of performances in GSM8k (still below in MATH, but greatly improved).
The authors then evaluate the models on harder benchmarks. MCTSr improves model performance across all of them. They notice that on Math Odyssey, the 8-rollout MCTSr is on the level of GPT-4 !
Prompts can be found within the appendix.
Code is open-sourced at: GitHub - trotsky1997/MathBlackBox
Personal Thoughts: While this research remains on preliminary stage, the results are quite impressive for results they get only by prompting. The fact a mere 8B model can reach frontier-levels of performance in benchmarks is nothing to laugh at. Still tells us there’s a lot of stuff to discover even solely with LLMs!
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
A prompt-level formula to add Search to LLM
Read of the day, day 85: Accessing GPT-4 level Mathematical Olympiad Solutions Via Monte Carlo Tree Self-refine with Llama-3 8B: A technical report, by Zhang et al from Shanghai Artificial Intelligence Laboratoryhttps://arxiv.org/pdf/2406.07394
The authors of this paper introduce a Monte-Carlo Tree Search like method to enhance model generation. They call it Monte-Carlo Tree Self-Refined, shortened as MCTSr.
Their method is based solely on prompting the model and does not modify its weight, yet greatly enhances the results.
How?
1- Generate a root node through naive answers or a dummy one
2- Use a value function Q to rank answers that were not expanded, select the best greedily
3- Optimize answer through generating a feedback, and then exploit it
4- Compute the Q value of the answer
5- Update value of parent nodes
6- Identify candidate nodes for expansion, and use UCT formula to update all nodes for iterating again
7- Iterate until max steps are reached
Value function Q is actually prompting the model to reward its answer. Model is prompted several times and its answers are averaged. Backpropagation and UCT formulas can be found within the paper.
The authors then evaluate 4 rollouts and 8 rollouts MCTSr on a Llama-3 8B and compare it to GPT-4, Claude 3 Opus and Gemini-1.5 Pro on mathematical problems.
They first find out such sampling greatly increases performances on both GSM8k and MATH datasets, reaching Frontier-models level of performances in GSM8k (still below in MATH, but greatly improved).
The authors then evaluate the models on harder benchmarks. MCTSr improves model performance across all of them. They notice that on Math Odyssey, the 8-rollout MCTSr is on the level of GPT-4 !
Prompts can be found within the appendix.
Code is open-sourced at: GitHub - trotsky1997/MathBlackBox
Personal Thoughts: While this research remains on preliminary stage, the results are quite impressive for results they get only by prompting. The fact a mere 8B model can reach frontier-levels of performance in benchmarks is nothing to laugh at. Still tells us there’s a lot of stuff to discover even solely with LLMs!
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Last edited:
Talk in any language or voice 
Be designed for any use case 
Handle millions of calls simultaneously. 24/7.
!
