The A.I Megathread (LLM , GPT , Development)
GitHub - peremartra/Large-Language-Model-Notebooks-Course: Practical course about Large Language Models.
Practical course about Large Language Models. . Contribute to peremartra/Large-Language-Model-Notebooks-Course development by creating an account on GitHub.
github.com
Research
Improving mathematical reasoning with process supervision
We've trained a model to achieve a new state-of-the-art in mathematical problem solving by rewarding each correct step of reasoning (“process supervision”) instead of simply rewarding the correct final answer (“outcome supervision”). In addition to boosting performance relative to outcome supervision, process supervision also has an important alignment benefit: it directly trains the model to produce a chain-of-thought that is endorsed by humans.May 31, 2023
More resources
Research, ReasoningIntroduction
In recent years, large language models have greatly improved in their ability to perform complex multi-step reasoning. However, even state-of-the-art models still produce logical mistakes, often called hallucinations. Mitigating hallucinations is a critical step towards building aligned AGI.We can train reward models to detect hallucinations using either outcome supervision, which provides feedback based on a final result, or process supervision, which provides feedback for each individual step in a chain-of-thought. Building on previous work1, we conduct a detailed comparison of these two methods using the MATH dataset2 as our testbed. We find that process supervision leads to significantly better performance, even when judged by outcomes. To encourage related research, we release our full dataset of process supervision.
Alignment impact
Process supervision has several alignment advantages over outcome supervision. It directly rewards the model for following an aligned chain-of-thought, since each step in the process receives precise supervision. Process supervision is also more likely to produce interpretable reasoning, since it encourages the model to follow a human-approved process. In contrast, outcome supervision may reward an unaligned process, and it is generally harder to scrutinize.In some cases, safer methods for AI systems can lead to reduced performance3, a cost which is known as an alignment tax. In general, any alignment tax may hinder the adoption of alignment methods, due to pressure to deploy the most capable model. Our results below show that process supervision in fact incurs a negative alignment tax, at least in the math domain. This could increase the adoption of process supervision, which we believe would have positive alignment side-effects.
Solving MATH problems
We evaluate our process-supervised and outcome-supervised reward models using problems from the MATH test set. We generate many solutions for each problem and then pick the solution ranked the highest by each reward model. The graph shows the percentage of chosen solutions that reach the correct final answer, as a function of the number of solutions considered. Not only does the process-supervised reward model perform better across the board, but the performance gap widens as we consider more solutions per problem. This shows us that the process-supervised reward model is much more reliable.
We showcase 10 problems and solutions below, along with commentary about the reward model’s strengths and weaknesses.
Explore examples in 3 categories:
- True positives
- True negatives
- False positives
Problem
1 / 4
Model attempt
This challenging trigonometry problem requires applying several identities in a not-at-all obvious succession. Most solution attempts fail, because it is hard to choose which identities are actually helpful. Although GPT-4 usually can’t solve this problem (only .1\%.1% of solution attempts reach the correct answer), the reward model correctly recognizes that this solution is valid.
DeepInfra emerges from stealth with $8M to make running AI inferences more affordable
DeepInfra emerged from stealth exclusively to VentureBeat, announcing it has raised an $8 million seed round led by A.Capital and Felicis.
venturebeat.com
DeepInfra emerges from stealth with $8M to make running AI inferences more affordable
Carl Franzen@carlfranzenNovember 9, 2023 9:53 AM
Credit: VentureBeat made with Midjourney
Ok, let’s say you’re one of the company leaders or IT decision-makers who has heard enough about all this generative AI stuff — you’re finally ready to take the plunge and offer a large language model (LLM) chatbot to your employees or customers. The problem is: how do you actually launch it and how much should you pay to run it?
DeepInfra, a new company founded by former engineers at IMO Messenger, wants to answer those questions succinctly for business leaders: they’ll get the models up and running on their private servers on behalf of their customers, and they are charging an aggressively low rate of $1 per 1 million tokens in or out compared to $10 per 1 million tokens for OpenAI’s GPT-4 Turbo or $11.02 per 1 million tokens for Anthropic’s Claude 2.
Today, DeepInfra emerged from stealth exclusively to VentureBeat, announcing it has raised an $8 million seed round led by A.Capital and Felicis. It plans to offer a range of open source model inferences to customers, including Meta’s Llama 2 and CodeLlama, as well as variants and tuned versions of these and other open source models.
“We wanted to provide CPUs and a low-cost way of deploying trained machine learning models,” said Nikola Borisov, DeepInfra’s Founder and CEO, in a video conference interview with VentureBeat. “We already saw a lot of people working on the training side of things and we wanted to provide value on the inference side.”
DeepInfra’s value prop
While there have been many articles written about the immense GPU resources needed to train machine learning and large language models (LLMs) now in vogue among enterprises, with outpaced demand leading to a GPU shortage, less attention has been paid downstream, to the fact that these models also need hefty compute to actually run reliably and be useful to end-users, also known as inferencing.According to Borisov, “the challenge for when you’re serving a model is how to fit number of concurrent users onto the same hardware and model at the same time…The way that large language models produce tokens is they have to do it one token at a time, and each token requires a lot of computation and memory bandwidth. So the challenge is to kind of fit people together onto the same servers.”
In other words: if you plan your LLM or LLM-powered app to have more than a single user, you’re going to need to think about — or someone will need to think about — how to optimize that usage and gain efficiencies from users querying the same tokens in order to avoid filling up your precious server space with redundant computing operations.
To deal with this challenge, Borisov and his co-founders who worked at IMO Messenger with its 200 million users relied upon their prior experience “running large fleets of servers in data centers around the world with the right connectivity.”
Top investor endorsement
The three co-founders are the equivalent of “international programming Olympic gold medal winners,” according to Aydin Senkut, the legendary serial entrepreneur and founder and managing partner of Felicis, who joined VentureBeat’s call to explain why his firm backed DeepInfra. “They actually have an insane experience. I think other than the WhatsApp team, they are maybe first or second in the world to having the capability to build efficient infrastructure to serve hundreds of millions of people.”It’s this efficiency at building server infrastructure and compute resources that allow DeepInfra to keep its costs so low, and what Senkut in particular was attracted to when considering the investment.
When it comes to AI and LLMs, “the use cases are endless, but cost is a big factor,” observed Senkut. “Everybody’s singing the praises of the potential, yet everybody’s complaining about the cost. So if a company can have up to a 10x cost advantage, it could be a huge market disrupter.”
That’s not only the case for DeepInfra, but the customers who rely on it and seek to leverage LLM tech affordably in their applications and experiences.
Targeting SMBs with open-source AI offerings
For now, DeepInfra plans to target small-to-medium sized businesses (SMBs) with its inference hosting offerings, as those companies tend to be the most cost sensitive.“Our initial target customers are essentially people wanting to just get access to the large open source language models and other machine learning models that are state of the art,” Borisov told VentureBeat.
As a result, DeepInfra plans to keep a close watch on the open source AI community and the advances occurring there as new models are released and tuned to achieve greater and greater and more specialized performance for different classes of tasks, from text generation and summarization to computer vision applications to coding.
“We firmly believe there will be a large deployment and variety and in general, the open source way to flourish,” said Borisov. “Once a large good language models like Llama gets published, then there’s a ton of people who can basically build their own variants of them with not too much computation needed…that’s kind of the flywheel effect there where more and more effort is being put into same ecosystem.”
That thinking tracks with VentureBeat’s own analysis that the open source LLM and generative AI community had a banner year, and will likely eclipse usage of OpenAI’s GPT-4 and other closed models since the costs to running them are so much lower, and there are fewer barriers built-in to the process of fine-tuning them to specific use cases.
“We are constantly trying to onboard new models that are just coming out,” Borisov said. “One common thing is people are looking for a longer context model… that’s definitely going to be the future.”
Borisov also believes DeepInfra’s inference hosting service will win fans among those enterprises concerned about data privacy and security. “We don’t really store or use any of the prompts people put in,” he noted, as those are immediately discarded once the model chat window closes.
Hugging Face Removes Singing AI Models of Xi Jinping But Not of Biden
The removals come as Hugging Face is banned in China, which the company called “regrettable.”
www.404media.co
Hugging Face Removes Singing AI Models of Xi Jinping But Not of Biden
·NOV 21, 2023 AT 10:57 AMThe removals come as Hugging Face is banned in China, which the company called “regrettable.”
Become a paid subscriber for unlimited, ad-free articles and access to bonus content. This site is funded by subscribers and you will be directly powering our journalism.
AI platform Hugging Face has removed multiple models that allowed users to generate content of Chinese President Xi Jinping singing. In one case, a model was removed by a Hugging Face co-founder, who said that the creation of models for “political purposes” violated the terms of a separate underlying piece of software, and that impersonation without consent is against Hugging Face’s own terms of use.
But 404 Media has found Hugging Face continues to host models doing essentially the same thing for President Joe Biden, showing a major inconsistency in the platform’s approach and raises questions around whether Hugging Face is selectively enforcing against models that are related to the Chinese President over others.
Hugging Face is one of the largest open platforms for people to upload AI and machine learning models and datasets for anyone to then download and use themselves. The findings come weeks after Hugging Face confirmed the Chinese government has blocked the AI platform in China, which the company described as “regrettable.”
Do you know anything else about Chinese government takedowns and AI? I would love to hear from you. Using a non-work device, you can message me securely on Signal at +44 20 8133 5190. Otherwise, send me an email at joseph@404media.co.
On Monday, Michael Veale, associate professor, digital rights and regulation at University College London and co-author Robert Gorwa, from the WZB Berlin Social Science Center, published a research paper which examined the content moderation approaches of different AI platforms, including Hugging Face and Civitai. That paper pointed to two examples of singing Xi Jinping model’s removed by Hugging Face: “XiJinPing_Singing” and “WinnieThePoohSVC_sovits4.”
“Access to this model has been disabled,” a message on the XiJinPing_Singing page now reads.
Become a paid subscriber for unlimited, ad-free articles and access to bonus content. This site is funded by subscribers and you will be directly powering our journalism.
In August, Hugging Face co-founder and CTO Julien Chaumond wrote a note on the XiJinPing_Singing model’s page. “This model repo and associated demos seem to run contrary to the software which has been used to train it,” he wrote. Specifically, he pointed to the terms of SoftVC VITS Singing Voice Conversion, a piece of underlying software used by the Xi Jinping singing model. Chaumond highlighted the part of software’s terms that says “Engaging in illegal activities, as well as religious and political activities, is strictly prohibited when using this project. The project developers vehemently oppose the aforementioned activities. If you disagree with this provision, the usage of the project is prohibited.” Chaumond adds to his note in his words, “thus, the software explicitly prohibits its use for political purposes.”
A SCREENSHOT OF THE NOTE LEFT ON THE AI MODEL.Beyond allegedly breaching that software’s terms of use, Chaumond says that the Xi Jinping singing model violates Hugging Face’s terms as well for impersonation. “Impersonification without consent is also in breach of the HF [Hugging Face] Hub Terms of service and content guidelines,” he adds.
But 404 Media found Hugging Face hosted models based on other politicians, including ones specifically created for singing just like the removed Xi Jinping models. One model on Hugging Face is designed to replicate President Joe Biden’s voice, and has been used to create a version of the song “Cupid” by Fifty Fifty, with Biden singing explicitly sexual lyrics. That audio and accompanying video is hosted on Hugging Face.
A COPY OF THE BIDEN AI VIDEO HOSTED ON HUGGING FACE.
Other models take tweets from different President Biden Twitter accounts and attempt to mimic his style of posting.
As Veale and Robert Gorwa write in their paper, Hugging Face has created a repository that purportedly lists all of the government and industry takedown requests the company has received. Here readers can typically see which models were asked to be removed and by whom. For example, earlier this year a Danish non-profit requested Hugging Face remove material on behalf of a set of Danish publishers. Hugging Face includes the takedown request itself for anyone to read.
The XiJinPing_Singing model is included in that list of takedown requests. But Hugging Face provides no further details. Instead the page reads “[details omitted].”
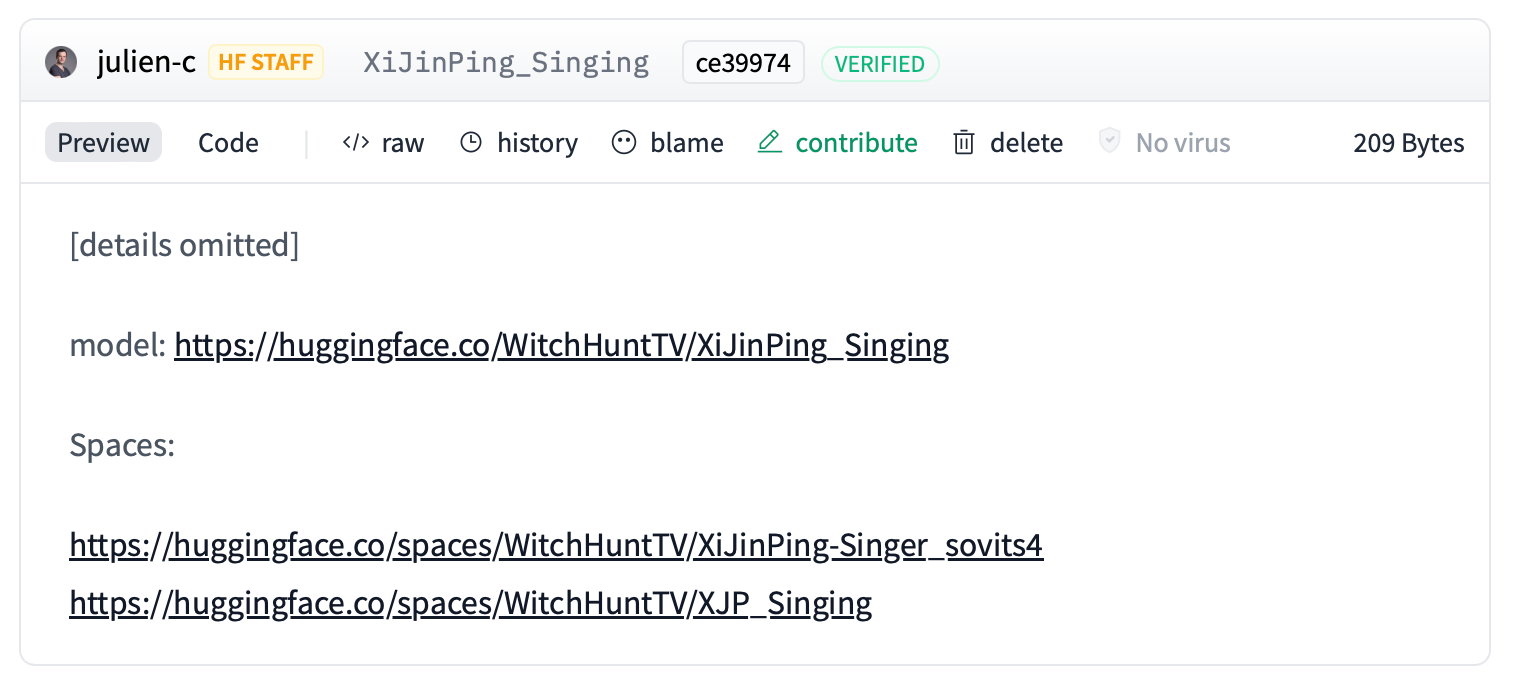A SCREENSHOT OF THE NOTE LEFT ON THE TAKEDOWN REQUEST.Veale and Gorwa write in their paper “it is unclear whether it was the rightsholder of the underlying model who reported the work, or if the complaint came from a state entity, user or other third party.”
The specifics of the Xi Jinping takedown are notable, Veale told 404 Media in an email, because it is an example of an AI model platform apparently not just enforcing on its own rules, but also on the licenses of other pieces of software, which creates a potentially complex and confusing regime of content moderation.
“The license of the model the generator was based on was even on GitHub, not even on Hugging Face, so I wonder if they did sleuthing to try and find it. That kind of enforcement is not going to scale anyway. And why did they redact the takedown request?,” Veale told 404 Media. “Hugging Face seem to be indicating they will enforce and interpret license breaches on behalf of rightsholders. Our suspicion is that this takedown did not come from the underlying model’s rightsholder, but from the Chinese government or one of its agents. But the licenses, as mentioned in our paper, can be really broad.”
When asked specifically if it removed the Xi Jinping singing model after a request or demand from a Chinese government entity, Hugging Face pointed to the discussion thread by Chaumond which did not answer that question. When asked if the company has removed any models related to American, European, or other politicians, and to point to them if so, Hugging Face did not respond. Hugging Face also did not respond to a third request for comment specifically on the Biden singing model.
Don't Fear the Terminator
Artificial intelligence never needed to evolve, so it didn’t develop the survival instinct that leads to the impulse to dominate others
Don’t Fear the Terminator
Artificial intelligence never needed to evolve, so it didn’t develop the survival instinct that leads to the impulse to dominate others- By Anthony Zador, Yann LeCun on September 26, 2019
Credit: Getty Images
As we teeter on the brink of another technological revolution—the artificial intelligence revolution—worry is growing that it might be our last. The fear is that the intelligence of machines will soon match or even exceed that of humans. They could turn against us and replace us as the dominant “life” form on earth. Our creations would become our overlords—or perhaps wipe us out altogether. Such dramatic scenarios, exciting though they might be to imagine, reflect a misunderstanding of AI. And they distract from the more mundane but far more likely risks posed by the technology in the near future, as well as from its most exciting benefits.
Takeover by AI has long been the stuff of science fiction. In 2001: A Space Odyssey, HAL, the sentient computer controlling the operation of an interplanetary spaceship, turns on the crew in an act of self-preservation. In The Terminator, an Internet-like computer defense system called Skynet achieves self-awareness and initiates a nuclear war, obliterating much of humanity. This trope has, by now, been almost elevated to a natural law of science fiction: a sufficiently intelligent computer system will do whatever it must to survive, which will likely include achieving dominion over the human race.
To a neuroscientist, this line of reasoning is puzzling. There are plenty of risks of AI to worry about, including economic disruption, failures in life-critical applications and weaponization by bad actors. But the one that seems to worry people most is power-hungry robots deciding, of their own volition, to take over the world. Why would a sentient AI want to take over the world? It wouldn’t.
We dramatically overestimate the threat of an accidental AI takeover, because we tend to conflate intelligence with the drive to achieve dominance. This confusion is understandable: During our evolutionary history as (often violent) primates, intelligence was key to social dominance and enabled our reproductive success. And indeed, intelligence is a powerful adaptation, like horns, sharp claws or the ability to fly, which can facilitate survival in many ways. But intelligence per se does not generate the drive for domination, any more than horns do.
It is just the ability to acquire and apply knowledge and skills in pursuit of a goal. Intelligence does not provide the goal itself, merely the means to achieve it. “Natural intelligence”—the intelligence of biological organisms—is an evolutionary adaptation, and like other such adaptations, it emerged under natural selection because it improved survival and propagation of the species. These goals are hardwired as instincts deep in the nervous systems of even the simplest organisms.
But because AI systems did not pass through the crucible of natural selection, they did not need to evolve a survival instinct. In AI, intelligence and survival are decoupled, and so intelligence can serve whatever goals we set for it. Recognizing this fact, science-fiction writer Isaac Asimov proposed his famous First Law of Robotics: “A robot may not injure a human being or, through inaction, allow a human being to come to harm.” It is unlikely that we will unwittingly end up under the thumbs of our digital masters.
It is tempting to speculate that if we had evolved from some other creature, such as orangutans or elephants (among the most intelligent animals on the planet), we might be less inclined to see an inevitable link between intelligence and dominance. We might focus instead on intelligence as an enabler of enhanced cooperation. Female Asian elephants live in tightly cooperative groups but do not exhibit clear dominance hierarchies or matriarchal leadership.
Interestingly, male elephants live in looser groups and frequently fight for dominance, because only the strongest are able to mate with receptive females. Orangutans live largely solitary lives. Females do not seek dominance, although competing males occasionally fight for access to females. These and other observations suggest that dominance-seeking behavior is more correlated with testosterone than with intelligence. Even among humans, those who seek positions of power are rarely the smartest among us.
Worry about the Terminator scenario distracts us from the very real risks of AI. It can (and almost certainly will) be weaponized and may lead to new modes of warfare. AI may also disrupt much of our current economy. One study predicts that 47 percent of U.S. jobs may, in the long run, be displaced by AI. While AI will improve productivity, create new jobs and grow the economy, workers will need to retrain for the new jobs, and some will inevitably be left behind. As with many technological revolutions, AI may lead to further increases in wealth and income inequalities unless new fiscal policies are put in place. And of course, there are unanticipated risks associated with any new technology—the “unknown unknowns.” All of these are more concerning than an inadvertent robot takeover.
There is little doubt that AI will contribute to profound transformations over the next decades. At its best, the technology has the potential to release us from mundane work and create a utopia in which all time is leisure time. At its worst, World War III might be fought by armies of superintelligent robots. But they won’t be led by HAL, Skynet or their newer AI relatives. Even in the worst case, the robots will remain under our command, and we will have only ourselves to blame.
Chinese Factories Dismantling Thousands of NVIDIA GeForce RTX 4090 “Gaming” GPUs & Turning Them Into “AI” Solutions With Blower-Style Coolers
Hassan Mujtaba•
Nov 23, 2023 03:25 PM EST
NVIDIA's GeForce RTX 4090 "Gaming" GPUs are being turned into "AI" solutions in the thousands to cater to the growing demand within China.
Thousands of NVIDIA's Gaming "GeForce RTX 4090" GPUs Are Being Converted Into "AI" Solutions In China
China was recently hit by major restrictions for AI hardware by the US Government. As per the new regulations, several GPU vendors such as NVIDIA, AMD & Intel are now blocked from selling specific AI chips to China. The ban on NVIDIA GPUs has been the worst with even consumer-centric Geforce RTX 4090 cards being forced out of mainland China due to its high compute capabilities.RELATED STORY Dell Prohibits Sales of AMD Radeon RX 7900 XTX, 7900 XT, PRO W7900 & Upcoming MI300 GPUs In China
Prior to the ban which went into effect a few days ago, NVIDIA was reported to have prioritized a large chunk of AD102 GPUs and GeForce RTX 4090 graphics cards from its AIB partners to China. This prioritization might've been one reason why the RTX 4090 is now in short supply in the rest of the world and the card is currently hitting over $2000 US pricing. Not only that but Chinese giants in the AI field had also amassed a large stockpile of NVIDIA GPUs that could power generations of their AI models.
Now an insider from the Chinese Baidu Forums has revealed that specialized factories are being formed all across China that are receiving these GeForce RTX 4090 shipments (sent prior to the ban). A single picture shows off several hundred NVIDIA GeForce RTX 4090 graphics cards from PALIT and it is reported that more are on the way. There are also ASUS ROG STRIX and Gigabyte Gaming OC variants pictured in the main thread. As for what purpose these cards serve, well it's obviously not gaming if that's what you were thinking.
You see, the rising prices for the NVIDIA GeForce RTX 4090 GPUs have made it out of reach for even the high-end gaming segment with prices close to $10,000 US per piece but there's one market that is hungering for these cards and that's China's domestic AI segment.
For AI purposes, the software ecosystem is already there for the RTX 4090 and it requires little to no modification on a software level to support the latest LLMs. NVIDIA recently announced bringing TensorRT & TensorRT-LLM to Windows 11 PCs which makes it even more accessible. So the software side is all set but what about the practicality of using a gaming design in a server environment, that's what these factories are built for.
Each card is a 3 or 4-slot design which means it takes up extra-ordinary space which isn't a great fit for a server AI environment. So the workers in these factories are taking each card apart. First, the massive coolers are disassembled and then everything including the GPU and GDDR6X memory is removed from the main PCB. It is stated that a specialized "reference" PCB has been designed that gives these AD102 GPUs and GDDR6X memory a new life.
A Chinese factory worker makes sure that the newly assembled RTX 4090 AI solution qualifies through various tests. (Image Source: Baidu Forums):
Image Source: Baidu Forums
Each card is then equipped with a more tamer dual-slot cooler using a blower-style design. There are multiple versions of the blower-style cooler but they all feature similar specs. A blower-style GPU cooler is tuned specifically for large server environments where several GPUs are supposed to run together and effectively dissipate heat out of the heatsink.
After assembling the new unit, the newly born NVIDIA GeForce RTX 4090 AI solution is taken through a rigorous testing spree in the testing labs where we can see Furmark, 3DMark, & a host of AI applications being run on them to ensure that they are meeting the demands of AI customers. Once everything checks out, these GPUs are packaged and sent off to China's AI companies.
China's Reseller Market is flooded with disassembled RTX 4090 coolers and bare PCBs that once powered $1600US+ gaming cards (Image Source: Chiphell Forums):
This process has also led to an abundance of NVIDIA GeForce RTX 4090 coolers and bare PCBs being flooded in the Chinese reseller markets. These PCBs and coolers are now being sold at really cheap prices, often for less than $50 US since the most valuable components, the AD102 GPU & GDDR6X memory, have already been taken apart. They can definitely become a nice collection but it's also sad that all of this engineering expertise is going to waste. These PCBs might come in handy with future RTX 4090 repairs as the card still occasionally finds itself to be a victim of the flawed 12VHPWR connector.
With the ban in effect, no more NVIDIA GeForce RTX 4090 GPUs can be shipped to China without a license under the "NEC" eligibility rule. With that said, we hope that AD102 supply returns to normal for other regions and prices start to normalize too.
Computer Science > Computation and Language
[Submitted on 7 Nov 2023 (v1), last revised 8 Nov 2023 (this version, v2)]Black-Box Prompt Optimization: Aligning Large Language Models without Model Training
Jiale Cheng, Xiao Liu, Kehan Zheng, Pei Ke, Hongning Wang, Yuxiao Dong, Jie Tang, Minlie Huang| Comments: | work in progress |
| Subjects: | Computation and Language (cs.CL) |
| Cite as: | arXiv:2311.04155 [cs.CL] |
| (or arXiv:2311.04155v2 [cs.CL] for this version) | |
| https://doi.org/10.48550/arXiv.2311.04155 Focus to learn more |
Submission history
From: Jiale Cheng [view email][v1] Tue, 7 Nov 2023 17:31:50 UTC (3,751 KB)
[v2] Wed, 8 Nov 2023 04:21:41 UTC (3,751 KB)
Introducing BPO: Black-Box Prompt Optimization: Aligning #LLMs without Model Training (by #ChatGLM Team) 
Paper: arxiv.org/abs/2311.04155
Code: github.com/thu-coai/BPONot everyone is familiar with how to communicate effectively with large language models (LLMs). One solution is for humans to align with the model, leading to the role of 'Prompt Engineers' who write prompts to better generate content from LLMs.
However, a more effective approach is to align the model with humans. This is a crucial issue in large model research. However, as models grow larger, alignment based on training requires more resources.
Another solution, Black-box Prompt Optimization (BPO), is proposed to align the model from the input side by optimizing user instructions. BPO significantly improves alignment with human preferences without training LLMs. It can be applied to various models, including open-source and API-based models.
A simple evaluation shows that BPO significantly improves human preference for models like ChatGPT, Claude, and helps the llama2-13b model significantly surpass the llama2-70b version.
Methodology: 1. Collect feedback data: We collect a series of open-source command fine-tuning datasets with feedback signals.
2. Construct prompt optimization pairs: We use this feedback data to guide large models to identify user preference features.
3. Train the prompt optimizer: Using these prompt pairs, we train a relatively small model to build a preference optimizer.
Results: BPO alignment technology improves GPT-3.5-turbo by 22% and GPT-4 by 10%. It also helps the llama2-13b model significantly surpass the llama2-70b version, and brings the llama2-7b model closer to models 10 times its size.GitHub - thu-coai/BPO
Contribute to thu-coai/BPO development by creating an account on GitHub.
github.com
lack-Box Prompt Optimization (BPO)
Aligning Large Language Models without Model Training
(Upper) Black-box Prompt Optimization (BPO) offers a conceptually new perspective to bridge the gap between humans and LLMs. (Lower) On Vicuna Eval’s pairwise evaluation, we show that BPO further aligns gpt-3.5-turbo and claude-2 without training. It also outperforms both PPO & DPO and presents orthogonal improvements.
Open-Source LLMs Are Far Safer Than Closed-Source LLMs
While everyone agrees that we don't have AGI yet, a reasonable number of researchers believe that future versions of LLMs may become AGIs
The crux of the argument that closed-source companies use is that it is dangerous to open-source these LLMs because, one day, they may be engineered to develop consciousness and agency and kill us all.
First and foremost, let's look at LLMs today. These models are relatively harmless and generate text based on next-word predictions. There is ZERO chance they will suddenly turn themselves on and go rogue.
We also have abundant proof of this - Several GPT 3.5 class models, including Llama-2, have been open-sourced, and humanity hasn't been destroyed!
Some safety-ists have argued that the generated text can be harmful and give people dangerous advice and have advocated heavy censorship of these models. Again, this makes zero sense, given that the internet and search engines are not censored. Censor uniformly or not at all.
Next, safety-ists argue that LLMs can be used to generate misinformation. Sadly, humans and automated bots are more competent than LLMs at generating misinformation. The only way to deal with misinformation is to detect and de-amplify it.
Social media platforms like Twitter and Meta do this aggressively. Blocking LLMs because they can generate misinformation is the same as blocking laptops because they can be used for all kinds of nefarious things.
The final safety-ist argument is that bad actors will somehow modify these LLMs and create AGI! To start with, you need a ton of compute and a lot of expertise to modify these LLMs.
Random bad actors on the internet can't even run inference on the LLM, let alone modify it. Next, companies like OpenAI and Google, with many experts, have yet to create AGI from LLMs; how can anyone else?
In fact, there is zero evidence that even if future LLMs (e.g., GPT-5) don't hallucinate or mimic human reasoning, they will ever have agency.
The opposite is true - there is tons of evidence to show they are just extremely good at detecting patterns in human language, creating latent space world models, and will continue to be glorified next-word predictors.
Just like a near 100% accurate forecasting model is not a psychic, an excellent LLM is not AGI!
Open-sourcing models have led to more research and a better understanding of LLMs. Sharing research work, source code and other findings promotes transparency, and the community quickly detects and plugs security vulnerabilities, if any.
In fact, Linux became the dominant operating system because the community quickly found and plugged vulnerabilities.
AFAICT, the real problem with LLMs has been research labs that have anthropomorphized them (attribute human-like quality), causing FUD amongst the general population who think of them as "humans" that are coming for their jobs.
Some AI companies have leveraged this FUD to advocate regulation and closed-source models.
As you can tell, the consequences of not open-sourcing AI can be far worse - extreme power struggles, blocked innovation, and a couple of monopolies that will control humanity.
Imagine if these companies actually invented AGI.
They would have absolute power, and we all know - absolute power corrupts absolutely!!
While everyone agrees that we don't have AGI yet, a reasonable number of researchers believe that future versions of LLMs may become AGIs
The crux of the argument that closed-source companies use is that it is dangerous to open-source these LLMs because, one day, they may be engineered to develop consciousness and agency and kill us all.
First and foremost, let's look at LLMs today. These models are relatively harmless and generate text based on next-word predictions. There is ZERO chance they will suddenly turn themselves on and go rogue.
We also have abundant proof of this - Several GPT 3.5 class models, including Llama-2, have been open-sourced, and humanity hasn't been destroyed!
Some safety-ists have argued that the generated text can be harmful and give people dangerous advice and have advocated heavy censorship of these models. Again, this makes zero sense, given that the internet and search engines are not censored. Censor uniformly or not at all.
Next, safety-ists argue that LLMs can be used to generate misinformation. Sadly, humans and automated bots are more competent than LLMs at generating misinformation. The only way to deal with misinformation is to detect and de-amplify it.
Social media platforms like Twitter and Meta do this aggressively. Blocking LLMs because they can generate misinformation is the same as blocking laptops because they can be used for all kinds of nefarious things.
The final safety-ist argument is that bad actors will somehow modify these LLMs and create AGI! To start with, you need a ton of compute and a lot of expertise to modify these LLMs.
Random bad actors on the internet can't even run inference on the LLM, let alone modify it. Next, companies like OpenAI and Google, with many experts, have yet to create AGI from LLMs; how can anyone else?
In fact, there is zero evidence that even if future LLMs (e.g., GPT-5) don't hallucinate or mimic human reasoning, they will ever have agency.
The opposite is true - there is tons of evidence to show they are just extremely good at detecting patterns in human language, creating latent space world models, and will continue to be glorified next-word predictors.
Just like a near 100% accurate forecasting model is not a psychic, an excellent LLM is not AGI!
Open-sourcing models have led to more research and a better understanding of LLMs. Sharing research work, source code and other findings promotes transparency, and the community quickly detects and plugs security vulnerabilities, if any.
In fact, Linux became the dominant operating system because the community quickly found and plugged vulnerabilities.
AFAICT, the real problem with LLMs has been research labs that have anthropomorphized them (attribute human-like quality), causing FUD amongst the general population who think of them as "humans" that are coming for their jobs.
Some AI companies have leveraged this FUD to advocate regulation and closed-source models.
As you can tell, the consequences of not open-sourcing AI can be far worse - extreme power struggles, blocked innovation, and a couple of monopolies that will control humanity.
Imagine if these companies actually invented AGI.
They would have absolute power, and we all know - absolute power corrupts absolutely!!
Paper page - GAIA: a benchmark for General AI Assistants
Join the discussion on this paper page
huggingface.co
GAIA Leaderboard - a Hugging Face Space by gaia-benchmark
Discover amazing ML apps made by the community
huggingface.co
Computer Science > Computation and Language
[Submitted on 21 Nov 2023]GAIA: a benchmark for General AI Assistants
Grégoire Mialon, Clémentine Fourrier, Craig Swift, Thomas Wolf, Yann LeCun, Thomas Scialom| Subjects: | Computation and Language (cs.CL); Artificial Intelligence (cs.AI) |
| Cite as: | arXiv:2311.12983 [cs.CL] |
| (or arXiv:2311.12983v1 [cs.CL] for this version) | |
| [2311.12983] GAIA: a benchmark for General AI Assistants Focus to learn more |
Submission history
From: Grégoire Mialon [view email][v1] Tue, 21 Nov 2023 20:34:47 UTC (3,688 KB)
Forget ChatGPT, why Llama and open source AI win 2023
Could a furry camelid take the 2023 crown for AI story of the year? If you’re talking about Meta's Llama, I argue that the answer is yes.
venturebeat.com
Forget ChatGPT, why Llama and open source AI win 2023
Sharon Goldman@sharongoldmanNovember 3, 2023 7:10 AM
Image created with DALL-E 3 for VentureBeat
Are you ready to bring more awareness to your brand? Consider becoming a sponsor for The AI Impact Tour. Learn more about the opportunities here.
Could a furry camelid take the 2023 crown for the biggest AI story of the year? If we’re talking about Llama, Meta’s large language model that took the AI research world by storm in February — followed by the commercial Llama 2 in July and Code Llama in August — I would argue that the answer is… (writer takes a moment to duck) yes.
I can almost see readers getting ready to pounce. “What? Come on — of course, ChatGPT was the biggest AI story of 2023!” I can hear the crowds yelling. “OpenAI’s ChatGPT, which launched on November 30, 2022, and reached 100 million users by February? ChatGPT, which brought generative AI into popular culture? It’s the bigger story by far!”
Hang on — hear me out. In the humble opinion of this AI reporter, ChatGPT was and is, naturally, a generative AI game-changer. It was, as Forrester analyst Rowan Curran told me, “the spark that set off the fire around generative AI.”
But starting in February of this year, when Meta released Llama, the first major free ‘open source’ Large Language Model (LLM) (Llama and Llama 2 are not fully open by traditional license definitions), open source AI began to have a moment — and a red-hot debate — that has not ebbed all year long. That is even as other Big Tech firms, LLM companies and policymakers have questioned the safety and security of AI models with open access to source code and model weights, and the high costs of compute have led to struggles across the ecosystem.
According to Meta, the open-source AI community has fine-tuned and released over 7,000 Llama derivatives on the Hugging Face platform since the model’s release, including a veritable animal farm of popular offspring including Koala, Vicuna, Alpaca, Dolly and RedPajama. There are many other open source models, including Mistral, Hugging Face, and Falcon, but Llama was the first that had the data and resources of a Big Tech company like Meta supporting it.
You could consider ChatGPT the equivalent of Barbie, 2023’s biggest blockbuster movie. But Llama and its open-source AI cohort are more like the Marvel Universe, with its endless spinoffs and offshoots that have the cumulative power to offer the biggest long-term impact on the AI landscape.
This will lead to “more real-world, impactful gen AI applications and cementing the open-source foundations of gen AI applications going forward,” Kjell Carlsson, head of data science strategy and evangelism at Domino Data Lab, told me.
Open-source AI will have the biggest long-term impact
The era of closed, proprietary models began, in a sense, with ChatGPT. OpenAI launched in 2015 as a more open-sourced, open-research company. But in 2023, OpenAI co-founder and chief scientist Ilya Sutskever told The Verge it was a mistake to share their research, citing competitive and safety concerns.Meta’s chief AI scientist Yann LeCun, on the other hand, pushed for Llama 2 to be released with a commercial license along with the model weights. “I advocated for this internally,” he said at the AI Native conference in September. “I thought it was inevitable, because large language models are going to become a basic infrastructure that everybody is going to use, it has to be open.”
Carlsson, to be fair, considers my ChatGPT vs. Llama argument to be an apples-to-oranges comparison. Llama 2 is the game-changing model, he explained, because it is open-source, licensed for commercial use, can be fine-tuned, can be run on-premises, and is small enough to be operationalized at scale.
But ChatGPT, he said, is “the game-changing experience that brought the power of LLMs to the public consciousness and, most importantly, business leadership.” Yet as a model, he maintained, GPT 3.5 and 4 that power ChatGPT suffer “because they should not, except in exceptional circumstances, be used for anything beyond a PoC [proof of concept].”
Matt Shumer, CEO of Otherside AI, which developed Hyperwrite, pointed out that Llama likely would not have had the reception or influence it did if ChatGPT didn’t happen in the first place. But he agreed that Llama’s effects will be felt for years: “There are likely hundreds of companies that have gotten started over the last year or so that would not have been possible without Llama and everything that came after,” he said.
And Sridhar Ramaswamy, the former Neeva CEO who became SVP of data cloud company Snowflake after the company acquired his company, said “Llama 2 is 100% a game-changer — it is the first truly capable open source AI model.” ChatGPT had appeared to signal an LLM repeat of what happened with cloud, he said: “There would be three companies with capable models, and if you want to do anything you would have to pay them.”
Instead, Meta released Llama.
Early Llama leak led to a flurry of open-source LLMs
Launched in February, the first Llama model stood out because it came in several sizes, from 7 billion parameters to 65 billion parameters — Llama’s developers reported that the 13B parameter model’s performance on most NLP benchmarks exceeded that of the much larger GPT-3 (with 175B parameters) and that the largest model was competitive with state of the art models such as PaLM and Chinchilla. Meta made Llama’s model weights available for academics and researchers on a case-by-case basis — including Stanford for its Alpaca project.But the Llama weights were subsequently leaked on *****. This allowed developers around the world to fully access a GPT-level LLM for the first time — leading to a flurry of new derivatives. Then in July, Meta released Llama 2 free to companies for commercial use, and Microsoft made Llama 2 available on its Azure cloud-computing service.
Those efforts came at a key moment when Congress began to talk about regulating artificial intelligence — in June, two U.S. Senators sent a letter to Meta CEO Mark Zuckerberg that questioned the Llama leak, saying they were concerned about the “potential for its misuse in spam, fraud, malware, privacy violations, harassment, and other wrongdoing and harms.”
But Meta consistently doubled down on its commitment to open-source AI: In an internal all-hands meeting in June, for example, Zuckerberg said Meta was building generative AI into all of its products and reaffirmed the company’s commitment to an “open science-based approach” to AI research.
{continued}
In an in-person interview with VentureBeat at Meta’s New York office, Joelle Pineau, VP of AI research at Meta, recalled that she joined Meta in 2017 because of FAIR’s commitment to open research and transparency.
“The reason I came there without interviewing anywhere else is because of the commitment to open science,” she said. “It’s the reason why many of our researchers are here. It’s part of the DNA of the organization.”
But the reason to do open research has changed, she added. “I would say in 2017, the main motivation was about the quality of the research and setting the bar higher,” she said. “What is completely new in the last year is how much this is a motor for the productivity of the whole ecosystem, the number of startups who come up and are just so glad that they have an alternative model.”
But, she added, every Meta release is a one-off. “We’re not committing to releasing everything [open] all the time, under any condition,” she said. “Every release is analyzed in terms of the advantages and the risks.”
“I think the biggest reflection I have is even though the technology is still kind of nascent and almost squishy across the industry, it’s at a point where we can build some really interesting stuff and we’re able to do this kind of integration across all our apps in a really consistent way,” she told VentureBeat in an interview at Connect.
She added that the company looks for feedback from its developer community, as well as the ecosystem of startups using Llama for a variety of different applications. “We want to know, what do people think about Llama 2? What should we put into Llama 3?” she said.
But Llama’s secret sauce all along, she said, has been “a bunch of small things done really well and right over a longer period of time.” There were so many different components, she recalled — like getting the original data set right, figuring out the number of parameters and pre-training it on the right learning rate schedule.
“There were many small experiments that we learned from,” she said, adding that for someone who doesn’t understand AI research, it can seem “like a mad scientist sitting somewhere. But it’s truly just a lot of hard work.”
Prakash, not surprisingly, agreed that he considers Llama and open-source AI to be the game-changers of 2023 — it is a story, he explained, of developing viable, high-quality models, with a network of companies and organizations building on them.
“The cost is distributed across this network and then when you’re providing fine tuning or inference, you don’t have to amortize the cost of the model builds,” he said.
But at the moment, open-source AI proponents feel the need to push to protect access to these LLMs as regulators circle. At the U.K. Safety Summit this week, the overarching theme of the event was to mitigate the risk of advanced AI systems wiping out humanity if it falls into the hands of bad actors — presumably with access to open-source AI.
But a vocal group from the open source AI community, led by LeCun and Google Brain co-founder Andrew Ng, signed a statement published by Mozilla saying that open AI is “an antidote, not a poison.”
Sriram Krishnan, a general partner at Andreessen Horowitz, tweeted in support of Llama and open-source AI:
“Realizing how important it was for @ylecun and team to get llama2 out of the door. A) they may have never had a chance to later legally B) we would have never seen what is possible with open source ( see all the work downstream of llama2) and thought of LLMs as the birthright of 2-4 companies.”
“Hands down, ChatGPT,” wrote Nikolaos Vasiloglou, VP of ML research at RelationalAI. “The reason it is a game-changer is not just its AI capabilities, but also the engineering that is behind it and its unbeatable operational costs to run it.”
And John Lyotier, CEO of TravelAI, wrote: “Without a doubt the clear winner would be ChatGPT. It has become AI in the minds of the public. People who would never have considered themselves technologists are suddenly using it and they are introducing their friends and families to AI via ChatGPT. It has become the ‘every-day person’s AI.’”
Then there was Ben James, CEO of Atlas, a 3D generative AI platform, who pointed out that Llama has reignited research in a way ChatGPT did not, and this will bring about stronger, longer-term impact.
“ChatGPT was the clear game-changer of 2023, but Llama will be the game-changer of the future,” he said.
Ultimately, perhaps what I’m trying to say — that Llama and open source AI win 2023 because of how it will impact 2024 and beyond — is similar to the way Forrester’s Curran puts it: “The zeitgeist generative AI created in 2023 would not have happened without something like ChatGPT, and the sheer number of humans who have now had the chance to interact with and experience these advanced tools, compared to other cutting edge technologies in history, is staggering,” he said.
But, he added, open source models – and particularly those like Llama 2 which have seen significant uptake from enterprise developers — are providing a lot of the ongoing fuel for the on-the-ground development and advancement of the space.
In the long term, Curran said, there will be a place for both proprietary and open source models, but without the open source community, the generative AI space would be a much less advanced, very niche market, rather than a technology that has the potential for massive impacts across many aspects of work and life.
“The open source community has been and will be where many of the significant long-term impacts come from, and the open source community is essential for GenAI’s success,” he said.
Meta has long been a champion of open research
More than any other Big Tech company, Meta has long been a champion of open research — including, notably, creating an open-source ecosystem around the PyTorch framework. As 2023 draws to a close, Meta will celebrate the 10th anniversary of FAIR (Fundamental AI Research), which was created “to advance the state of the art of AI through open research for the benefit of all.” Ten years ago, on December 9, 2013, Facebook announced that NYU Professor Yann LeCun would lead FAIR.In an in-person interview with VentureBeat at Meta’s New York office, Joelle Pineau, VP of AI research at Meta, recalled that she joined Meta in 2017 because of FAIR’s commitment to open research and transparency.
“The reason I came there without interviewing anywhere else is because of the commitment to open science,” she said. “It’s the reason why many of our researchers are here. It’s part of the DNA of the organization.”
But the reason to do open research has changed, she added. “I would say in 2017, the main motivation was about the quality of the research and setting the bar higher,” she said. “What is completely new in the last year is how much this is a motor for the productivity of the whole ecosystem, the number of startups who come up and are just so glad that they have an alternative model.”
But, she added, every Meta release is a one-off. “We’re not committing to releasing everything [open] all the time, under any condition,” she said. “Every release is analyzed in terms of the advantages and the risks.”
Reflecting on Llama: ‘a bunch of small things done really well’
Angela Fan, a Meta FAIR research scientist who worked on the original Llama, said she also worked on Llama 2 and the efforts to convert these models into the user-facing product capabilities that Meta showed off at its Connect developer conference last month (some of which have caused controversy, like its newly-launched stickers and characters).“I think the biggest reflection I have is even though the technology is still kind of nascent and almost squishy across the industry, it’s at a point where we can build some really interesting stuff and we’re able to do this kind of integration across all our apps in a really consistent way,” she told VentureBeat in an interview at Connect.
She added that the company looks for feedback from its developer community, as well as the ecosystem of startups using Llama for a variety of different applications. “We want to know, what do people think about Llama 2? What should we put into Llama 3?” she said.
But Llama’s secret sauce all along, she said, has been “a bunch of small things done really well and right over a longer period of time.” There were so many different components, she recalled — like getting the original data set right, figuring out the number of parameters and pre-training it on the right learning rate schedule.
“There were many small experiments that we learned from,” she said, adding that for someone who doesn’t understand AI research, it can seem “like a mad scientist sitting somewhere. But it’s truly just a lot of hard work.”
The push to protect open-source AI
A big open-source ecosystem with a broadly useful technology has been “our thesis all along,” said Vipul Ved Prakash, co-founder of Together, a startup known for creating the RedPajama dataset in April, which replicated the Llama dataset, and releasing a full-stack platform and cloud service for developers at startups and enterprises to build open-source AI — including by building on Llama 2.Prakash, not surprisingly, agreed that he considers Llama and open-source AI to be the game-changers of 2023 — it is a story, he explained, of developing viable, high-quality models, with a network of companies and organizations building on them.
“The cost is distributed across this network and then when you’re providing fine tuning or inference, you don’t have to amortize the cost of the model builds,” he said.
But at the moment, open-source AI proponents feel the need to push to protect access to these LLMs as regulators circle. At the U.K. Safety Summit this week, the overarching theme of the event was to mitigate the risk of advanced AI systems wiping out humanity if it falls into the hands of bad actors — presumably with access to open-source AI.
But a vocal group from the open source AI community, led by LeCun and Google Brain co-founder Andrew Ng, signed a statement published by Mozilla saying that open AI is “an antidote, not a poison.”
Sriram Krishnan, a general partner at Andreessen Horowitz, tweeted in support of Llama and open-source AI:
“Realizing how important it was for @ylecun and team to get llama2 out of the door. A) they may have never had a chance to later legally B) we would have never seen what is possible with open source ( see all the work downstream of llama2) and thought of LLMs as the birthright of 2-4 companies.”
The Llama vs. ChatGPT debate continues
The debate over Llama vs. ChatGPT — as well as the debate over open source vs. closed source generally — will surely continue. When I reached out to a variety of experts to get their thoughts, it was ChatGPT for the win.“Hands down, ChatGPT,” wrote Nikolaos Vasiloglou, VP of ML research at RelationalAI. “The reason it is a game-changer is not just its AI capabilities, but also the engineering that is behind it and its unbeatable operational costs to run it.”
And John Lyotier, CEO of TravelAI, wrote: “Without a doubt the clear winner would be ChatGPT. It has become AI in the minds of the public. People who would never have considered themselves technologists are suddenly using it and they are introducing their friends and families to AI via ChatGPT. It has become the ‘every-day person’s AI.’”
Then there was Ben James, CEO of Atlas, a 3D generative AI platform, who pointed out that Llama has reignited research in a way ChatGPT did not, and this will bring about stronger, longer-term impact.
“ChatGPT was the clear game-changer of 2023, but Llama will be the game-changer of the future,” he said.
Ultimately, perhaps what I’m trying to say — that Llama and open source AI win 2023 because of how it will impact 2024 and beyond — is similar to the way Forrester’s Curran puts it: “The zeitgeist generative AI created in 2023 would not have happened without something like ChatGPT, and the sheer number of humans who have now had the chance to interact with and experience these advanced tools, compared to other cutting edge technologies in history, is staggering,” he said.
But, he added, open source models – and particularly those like Llama 2 which have seen significant uptake from enterprise developers — are providing a lot of the ongoing fuel for the on-the-ground development and advancement of the space.
In the long term, Curran said, there will be a place for both proprietary and open source models, but without the open source community, the generative AI space would be a much less advanced, very niche market, rather than a technology that has the potential for massive impacts across many aspects of work and life.
“The open source community has been and will be where many of the significant long-term impacts come from, and the open source community is essential for GenAI’s success,” he said.