--&& Daily Math/Physics Questions Thread &&--
- Thread starter TheAnointedOne
- Start date
DrBanneker
Space is the Place
Difficulty: Medium
Category: Combinatorics
Assume that the probability of having a boy or girl is 50/50 (note: in real populations this is not true, sex ratio at birth slightly favors boys).
Assume a family decides to have four children. What is the probability (as a fraction) that they have:
1) All boys or all girls
2) 2 boys and 2 girls
Category: Combinatorics
Assume that the probability of having a boy or girl is 50/50 (note: in real populations this is not true, sex ratio at birth slightly favors boys).
Assume a family decides to have four children. What is the probability (as a fraction) that they have:
1) All boys or all girls
2) 2 boys and 2 girls
Serious Face
Pro
1) 1/16?
2) 6/16?
2) 6/16?
DrBanneker
Space is the Place
DrBanneker
Space is the Place
The way you solve the problem is using the binomial distribution
For the probability of "x" boys (or girls) out of "n" total childreen
(n,x) * (1/2)^x * (1/2)^(n-x)
(n,x) is the # of ways items x can be selected from n items with two choices
(n,x) = n!/(x!*(n-x)!) where ! designates a factorial calculation
For the probability of "x" boys (or girls) out of "n" total childreen
(n,x) * (1/2)^x * (1/2)^(n-x)
(n,x) is the # of ways items x can be selected from n items with two choices
(n,x) = n!/(x!*(n-x)!) where ! designates a factorial calculation
TheAnointedOne
Superstar
Difficulty: Easy
Category: Trig/Geometry
What is the total area of both squares?
Category: Trig/Geometry
What is the total area of both squares?
TheAnointedOne
Superstar
bump
DrBanneker
Space is the Place
Difficulty: Easy
Category: Trig/Geometry
What is the total area of both squares?
64?
R.E.N. Spells Ren
Veteran
Difficulty: Easy
Category: Trig/Geometry
What is the total area of both squares?
Easy? Perhaps to someone currently studying trig lol
I’m guessing it’s the same as the largest square that could fit in that semicircle....256/5=51.2?
Almost certainly wrong as it was way more complicated than it should’ve been for an “easy” question
edit: second guess, maybe it’s half of the largest square that could fit in a circle of that diameter. So, 64?
TheAnointedOne
Superstar
Hint
TheAnointedOne
Superstar
TheAnointedOne
Superstar
Easy? Perhaps to someone currently studying trig lol
I’m guessing it’s the same as the largest square that could fit in that semicircle....256/5=51.2?
Almost certainly wrong as it was way more complicated than it should’ve been for an “easy” question
edit: second guess, maybe it’s half of the largest square that could fit in a circle of that diameter. So, 64?
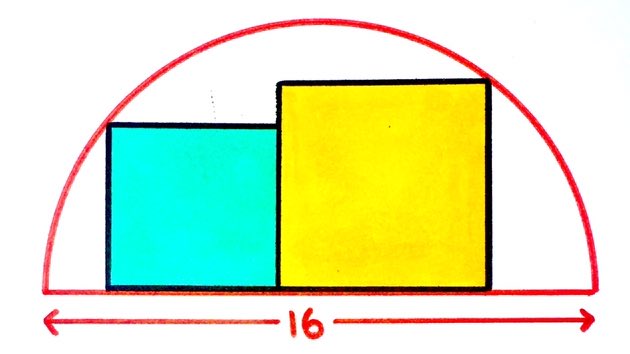
From the center of the half-circle to the outer rim is the radius. Which is 16 (the diameter) / 2 = 8.
Treat the whole thing as a polar coordinate system.
x^2 + y^2 = r^2
[8cos(theta)]^ + [8sin(theta)]^= 8^2
64*(cos(theta)^2 + sin(theta)^2) = 64
64*1 = 64
64 = 64
One side of the square then has to be sqrt(32)
sqrt(32) = sqrt(2)*sqrt(16) = 4*sqrt(2)
Area of one square = w*h = 4*sqrt(2)*4*sqrt(2) = 16*2 = 32
Both squares have the same area so: 32 + 32 = 64
R.E.N. Spells Ren
Veteran
This is what you call easy, breh??
I’ll share the logic I used since it’s completely different, but would’ve been what I used if I saw this on a test. First thing I noticed is that you didn’t give the dimensions of either square. This suggested to me that their dimensions didn’t matter. As long as you have two squares that touch the semicircle at one of their points and the base of the semicircle with one of their sides and one of their sides lined up with one of the sides of the other square then the total area of both squares would always be the same. So then I figured what would happen if I made the larger one smaller and the smaller one larger and still met the conditions laid out above....it would tend towards a rectangle...a rectangle that is half of the largest square that would fit in a full circle of the same diameter. The largest square that would fit in such a circle would have a diagonal equal to the diameter of the circle, 16. 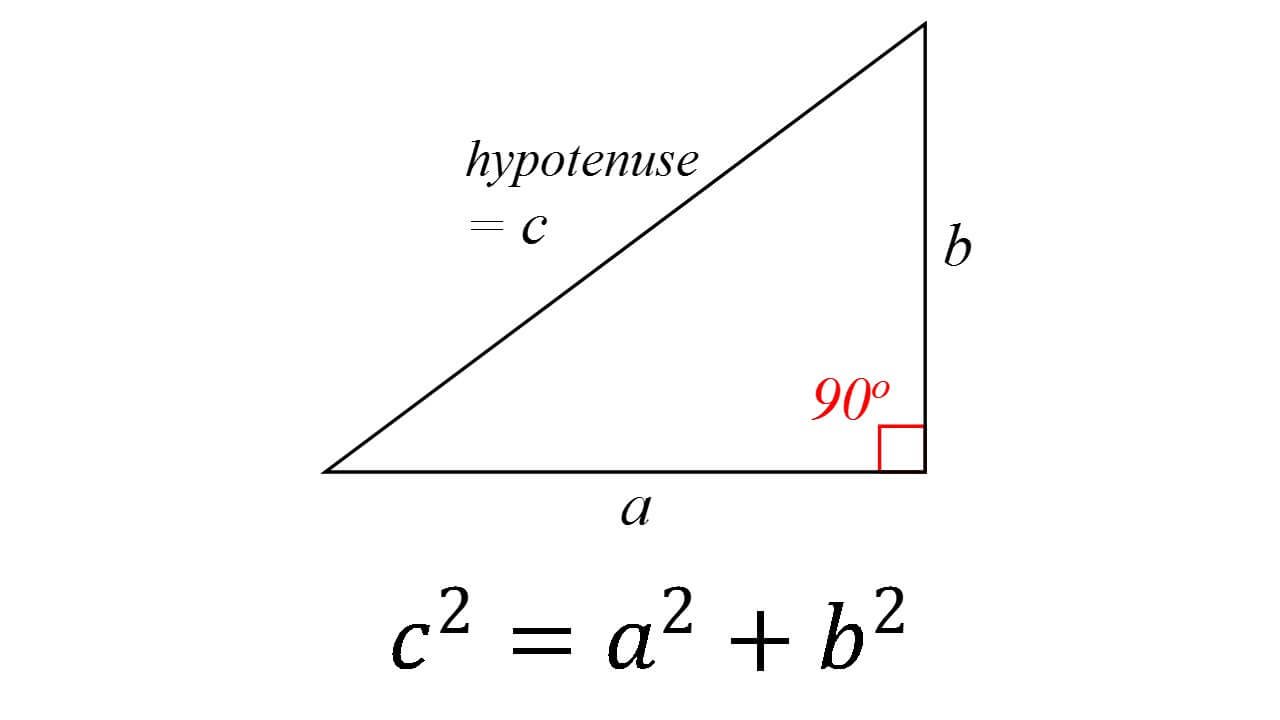Using Pythagoras' theorem:
I know that c = 16 and a = b (since it’s a square), thus
c^2 = a^2 + a^2
Or
c^2 = 2*a^2
thus
16^2=2*a^2
256=2*a^2
128=a^2
note that a^2=128 is also the area of this largest square that could fit in the full circle with a diameter of 16. But we want half of that to know what the area of the rectangle sitting in the semicircle is so that’s 128/2=64.
Wanted to share that cuz sometimes even if you don’t know the trig, knowing how to interpret what the question is and is not telling you can often help you find the answer using the math you do know. Using this principle really helped me excel in school. Saw many others struggle and give up in such situations.
I did have a question about your solution. Your closing line says...
...but both squares do not have the same area; unless the drawing is inaccurate. Can you expound?
Last edited:
TheAnointedOne
Superstar
Category: Physics
Difficulty: Easy
Vehicle #1 leaves a point at 3.00 p.m. at a rate of 25 mph. Vehicle #2 leaves the same point at 4:30 p.m. in the same direction at a rate of 30 mph. How long will it take Vehicle #2 to catch up with Vehicle #1?
Difficulty: Easy
Vehicle #1 leaves a point at 3.00 p.m. at a rate of 25 mph. Vehicle #2 leaves the same point at 4:30 p.m. in the same direction at a rate of 30 mph. How long will it take Vehicle #2 to catch up with Vehicle #1?
From 3:00pm to 4:30pm Vehicle #1 travels a total of 25 mph x 1.5 hours = 37.5 miles. Vehicle #2 catches up at the rate of 30 mph - 25 mph = 5 mph, so it would take 37.5 miles / 5 mph = 7.5 hours to catch up.