ogc163
Superstar
I’m in the mood to write about some econ papers today.
The most interesting one I’ve come across recently is Thomas Philippon’s working paper on “additive growth”. Back in April, he wrote a Twitter thread explaining the paper’s basic findings and arguments:
So, let me unpack this a bit for those who aren’t well-versed in the concepts already. Total Factor Productivity is the part of GDP that we can’t explain in terms of inputs like labor, capital, and land. An economist once called it “a measure of our ignorance”. And yet in the long term, TFP is the most important driver of growth in living standards, because we know we can max out all the other stuff. Once you put all the people to work and build all the buildings and machines and roads you need, you can only keep growing by using those inputs in a smarter way. That’s TFP.
Many people identify TFP with technology, which is obviously an important piece of it, but the two aren’t quite the same. In fact, we don’t know exactly what TFP is — we only know we want more of it.
Most economic models assume that TFP grows exponentially. The reason is partly that GDP itself often looks like it grows exponentially, but this assumption is also easy to work with mathematically (Never underestimate economists’ ability to convince themselves that the world works in a way that’s convenient for their equations!). But TFP might not grow exponentially. It might grow linearly — or “additively”, as Philippon puts it. TFP might be a straight upward line instead of curve that explodes upward faster and faster. Philippon plots two different measures of U.S. TFP growth since WW2, and finds that they look more like a straight line than an exponential curve:

The rest of the paper is basically just Philippon doing a bunch of checks to show you that no, your eyes aren’t tricking you, it really is just a straight line.
Economists have definitely noticed that the percentage growth rate of TFP has been slowing down in recent decades — it slowed in the 70s and 80s, accelerated again in the 90s and early 00s, then slowed back down. (Exponential curves have a constant percentage growth rate.) But they still maintained the belief that whatever underlying process drives growth was fundamentally exponential, and that the rate of exponential growth was simply falling. Now here comes Philippon and says no, it’s just that it was always a straight line all along.
Ahh, but was it a line all along? As many other observers have already noted, when Philippon extends the line back before WW2 for the U.S. and the UK, he finds that the slope of the line changed, probably multiple times:

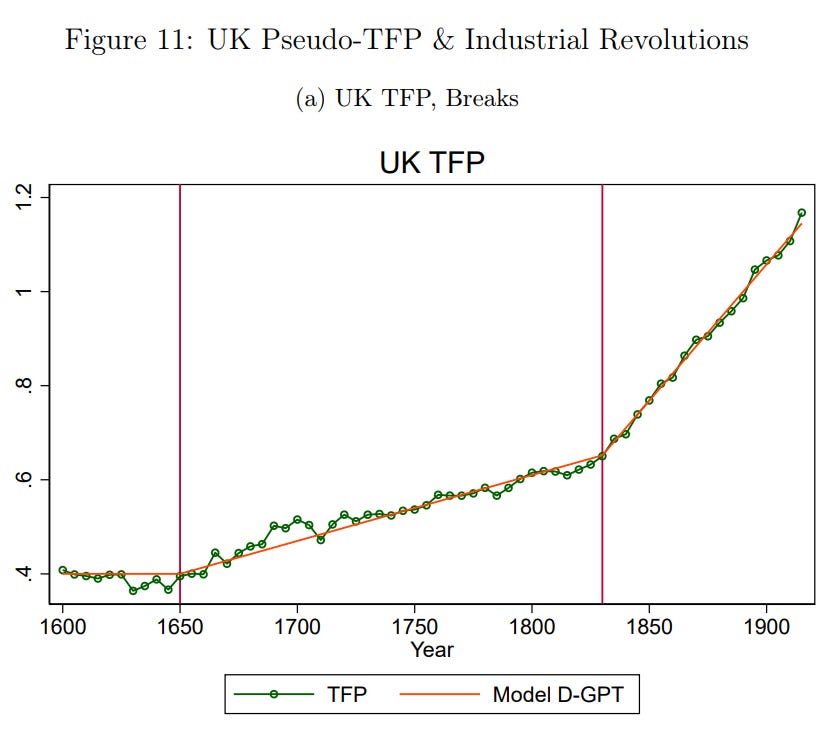
Philippon’s explanation for this is that growth is normally linear, but that it shifts each time a new general-purpose technology such as electrification or steam power arrives on the scene. (Yes, this is whyGoogle OpenAI punningly named their machine-learning language model “GPT-3”; they are hoping that machine learning is the new big paradigm.) Each new GPT, Philippon says, enables faster linear growth going forward.
So really the two models we’re looking at are not “exponential curve” vs. “straight line”. They’re “exponential curve that has recently slowed down because we’re discovering fewer new technologies” vs. “straight line that keeps getting faster each time a big new technology is discovered”. To be honest, I’m not sure those two models tell us such very different things about our world. In the first case, we can expect linear growth at about the current pace unless we discover another GPT. In the second case, we can expect exponential growth at a slower percentage rate than before unless we accelerate the pace of technological innovation. In both cases, the message is clear: Discover more useful technologies, or living standards won’t rise as much. Well, OK then. Let’s discover some awesome new technologies!
(By the way, I often say that macroeconomics is hard because we “don’t have enough data”. Well, this is exactly what I’m talking about. Even 4 centuries of data isn’t enough to tell us whether growth is linear or exponential!)
There’s also the question of why we would expect TFP growth to have any kind of long-term functional form in the first place. Why would it be either consistently linear or consistently exponential?
Exponential growth processes are typically things where “like begets like”. Population growth, for example, is exponential (in the absence of limiting factors), because people give rise to other people. It makes sense that per capita GDP growth would have an exponential component, because you use capital to build more capital. And indeed, as Dietz Vollrath has noted, U.S. GDP growth since WW2 does look a lot more exponential than TFP growth does.
But why would TFP work this way? Lots of economists have made various models to try to explain why TFP might be exponential — these usually involve combinatorial innovation, i.e. producing new ideas using old ideas. That makes conceptual sense — for example, you need to know how both electric current and semiconductors work in order to build a transistor. But there’s no real way to quantify or measure these ideas — all we can really measure is TFP itself. The “stock of ideas” is kind of this fantasy variable we think about in the background. So whether ideas “give birth” to other ideas at some constant rate is not something we’ll ever know.
And as Vollrath points out, the relationship between this imaginary “stock of ideas” and TFP itself could change over time. Even if ideas give birth to new ideas at a constant rate, each idea might increase TFP less than the one before it (maybe because we went for the most useful ideas first). Vollrath shows that if you assume that TFP is equal to the natural log of the number of ideas, and if ideas give birth to each other at a constant rate, you get perfectly linear growth. Cool result! But again, unless we someday figure out a way to measure the amount of “ideas” directly, all this is just sort of blowing smoke.
The most interesting one I’ve come across recently is Thomas Philippon’s working paper on “additive growth”. Back in April, he wrote a Twitter thread explaining the paper’s basic findings and arguments:
So, let me unpack this a bit for those who aren’t well-versed in the concepts already. Total Factor Productivity is the part of GDP that we can’t explain in terms of inputs like labor, capital, and land. An economist once called it “a measure of our ignorance”. And yet in the long term, TFP is the most important driver of growth in living standards, because we know we can max out all the other stuff. Once you put all the people to work and build all the buildings and machines and roads you need, you can only keep growing by using those inputs in a smarter way. That’s TFP.
Many people identify TFP with technology, which is obviously an important piece of it, but the two aren’t quite the same. In fact, we don’t know exactly what TFP is — we only know we want more of it.
Most economic models assume that TFP grows exponentially. The reason is partly that GDP itself often looks like it grows exponentially, but this assumption is also easy to work with mathematically (Never underestimate economists’ ability to convince themselves that the world works in a way that’s convenient for their equations!). But TFP might not grow exponentially. It might grow linearly — or “additively”, as Philippon puts it. TFP might be a straight upward line instead of curve that explodes upward faster and faster. Philippon plots two different measures of U.S. TFP growth since WW2, and finds that they look more like a straight line than an exponential curve:

The rest of the paper is basically just Philippon doing a bunch of checks to show you that no, your eyes aren’t tricking you, it really is just a straight line.
Economists have definitely noticed that the percentage growth rate of TFP has been slowing down in recent decades — it slowed in the 70s and 80s, accelerated again in the 90s and early 00s, then slowed back down. (Exponential curves have a constant percentage growth rate.) But they still maintained the belief that whatever underlying process drives growth was fundamentally exponential, and that the rate of exponential growth was simply falling. Now here comes Philippon and says no, it’s just that it was always a straight line all along.
Ahh, but was it a line all along? As many other observers have already noted, when Philippon extends the line back before WW2 for the U.S. and the UK, he finds that the slope of the line changed, probably multiple times:


Philippon’s explanation for this is that growth is normally linear, but that it shifts each time a new general-purpose technology such as electrification or steam power arrives on the scene. (Yes, this is why
So really the two models we’re looking at are not “exponential curve” vs. “straight line”. They’re “exponential curve that has recently slowed down because we’re discovering fewer new technologies” vs. “straight line that keeps getting faster each time a big new technology is discovered”. To be honest, I’m not sure those two models tell us such very different things about our world. In the first case, we can expect linear growth at about the current pace unless we discover another GPT. In the second case, we can expect exponential growth at a slower percentage rate than before unless we accelerate the pace of technological innovation. In both cases, the message is clear: Discover more useful technologies, or living standards won’t rise as much. Well, OK then. Let’s discover some awesome new technologies!
(By the way, I often say that macroeconomics is hard because we “don’t have enough data”. Well, this is exactly what I’m talking about. Even 4 centuries of data isn’t enough to tell us whether growth is linear or exponential!)
There’s also the question of why we would expect TFP growth to have any kind of long-term functional form in the first place. Why would it be either consistently linear or consistently exponential?
Exponential growth processes are typically things where “like begets like”. Population growth, for example, is exponential (in the absence of limiting factors), because people give rise to other people. It makes sense that per capita GDP growth would have an exponential component, because you use capital to build more capital. And indeed, as Dietz Vollrath has noted, U.S. GDP growth since WW2 does look a lot more exponential than TFP growth does.
But why would TFP work this way? Lots of economists have made various models to try to explain why TFP might be exponential — these usually involve combinatorial innovation, i.e. producing new ideas using old ideas. That makes conceptual sense — for example, you need to know how both electric current and semiconductors work in order to build a transistor. But there’s no real way to quantify or measure these ideas — all we can really measure is TFP itself. The “stock of ideas” is kind of this fantasy variable we think about in the background. So whether ideas “give birth” to other ideas at some constant rate is not something we’ll ever know.
And as Vollrath points out, the relationship between this imaginary “stock of ideas” and TFP itself could change over time. Even if ideas give birth to new ideas at a constant rate, each idea might increase TFP less than the one before it (maybe because we went for the most useful ideas first). Vollrath shows that if you assume that TFP is equal to the natural log of the number of ideas, and if ideas give birth to each other at a constant rate, you get perfectly linear growth. Cool result! But again, unless we someday figure out a way to measure the amount of “ideas” directly, all this is just sort of blowing smoke.