AI discovering new equations in physics

[bnew]

---

[2405.04484] OptPDE: Discovering Novel Integrable Systems via AI-Human Collaboration

Computer Science > Machine Learning​

[Submitted on 7 May 2024]

OptPDE - Discovering Novel Integrable Systems via AI-Human Collaboration​

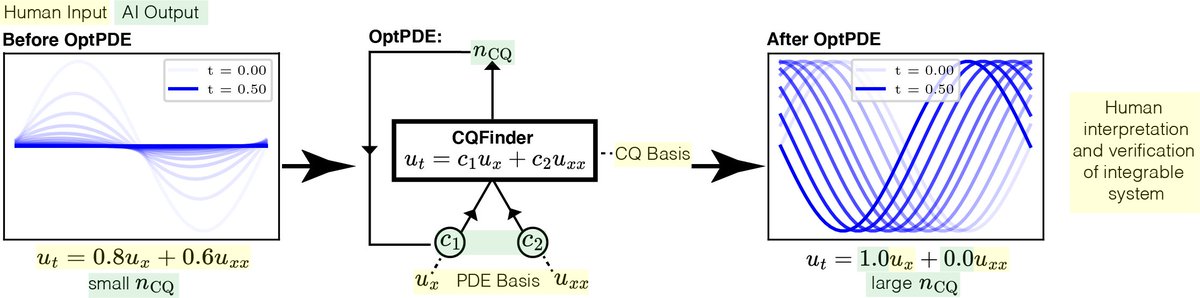
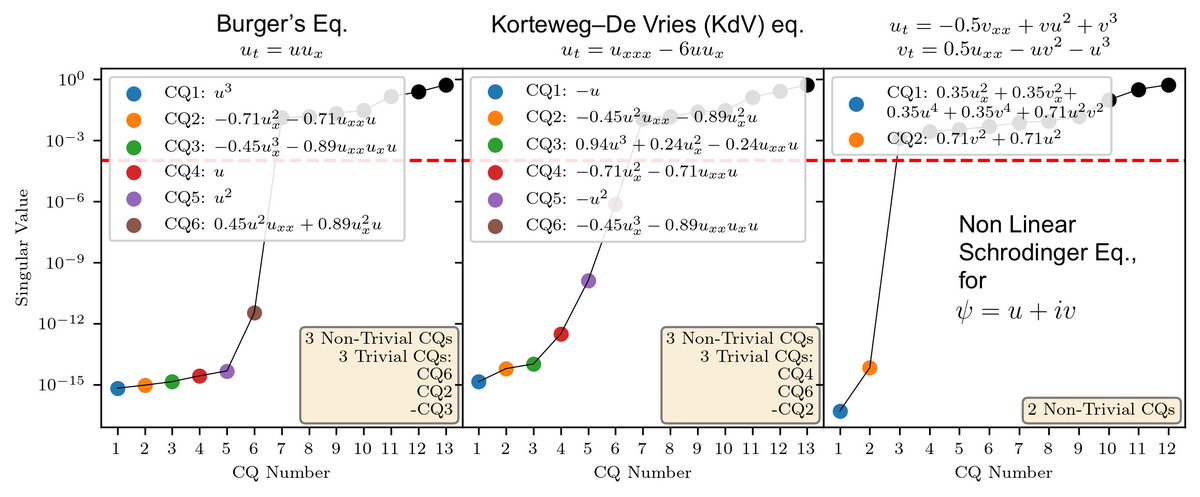
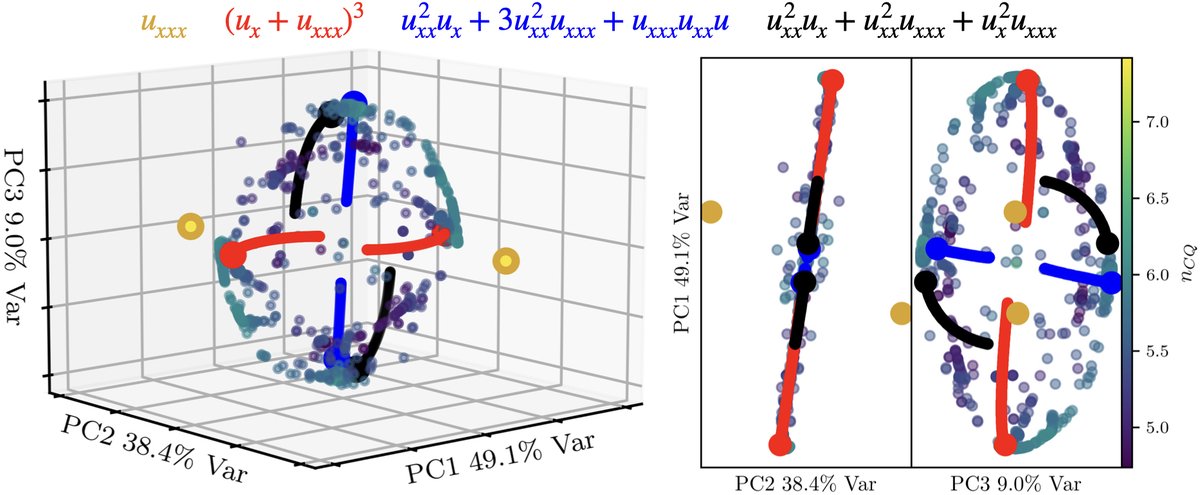
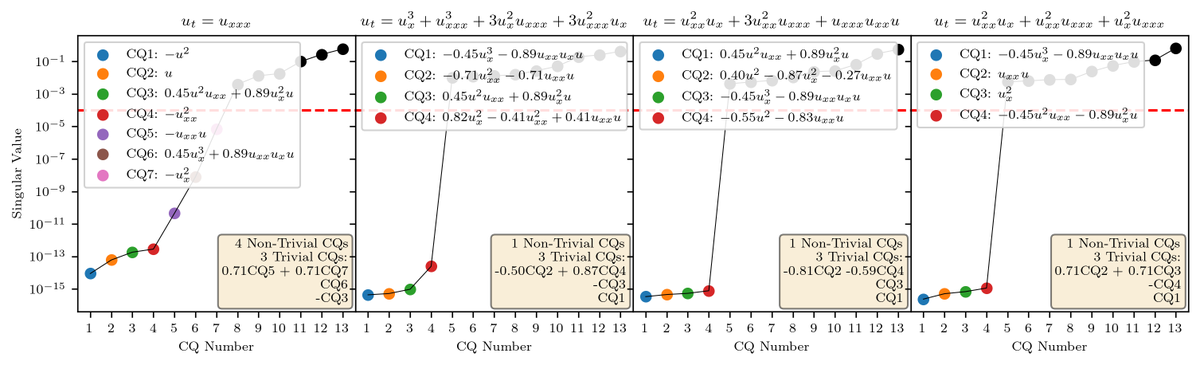
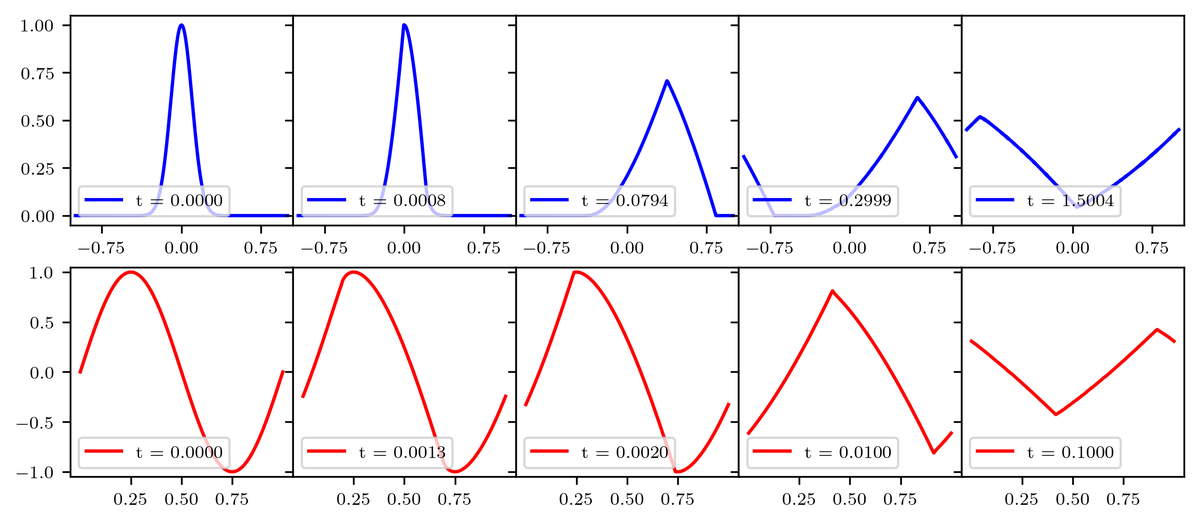
Subhash Kantamneni, Ziming Liu, Max Tegmark

Integrable partial differential equation (PDE) systems are of great interest in natural science, but are exceedingly rare and difficult to discover. To solve this, we introduce OptPDE, a first-of-its-kind machine learning approach that Optimizes PDEs' coefficients to maximize their number of conserved quantities, nCQ, and thus discover new integrable systems. We discover four families of integrable PDEs, one of which was previously known, and three of which have at least one conserved quantity but are new to the literature to the best of our knowledge. We investigate more deeply the properties of one of these novel PDE families, ut=(ux+a2uxxx)3. Our paper offers a promising schema of AI-human collaboration for integrable system discovery: machine learning generates interpretable hypotheses for possible integrable systems, which human scientists can verify and analyze, to truly close the discovery loop.

Subjects:	Machine Learning (cs.LG); Computational Physics (physics.comp-ph)
Cite as:	arXiv:2405.04484 [cs.LG]
	(or arXiv:2405.04484v1 [cs.LG] for this version)
	[2405.04484] OptPDE: Discovering Novel Integrable Systems via AI-Human Collaboration Focus to learn more

Submission history​

From: Subhash Kantamneni [view email]
[v1] Tue, 7 May 2024 16:53:29 UTC (2,879 KB)

https://arxiv.org/pdf/2405.04484

 

[bnew]

Spoiler: thread continued

Spoiler: full text

1/7
Integrable partial diff eqs (PDEs) are a physicist's bread and butter, but they're wildly rare and difficult to discover with pencil and paper.
To that end we unveil OptPDE - an AI system that discovers new, never before seen integrable PDEs!
@ZimingLiu11
@tegmark

2/7
1/N PDEs are integrable when they have conserved quantities (e.g. energy is a CQ for a mass-spring) so we design OptPDE as a two part system that can a) calculate the # of CQs for any PDE and b) find PDEs that maximize this n_CQ. Here's part a) in action on some familiar systems

3/7
2/N Our method to find n_CQ is differentiable, so to discover new integrable PDEs, we simply make the coefficients of terms in our PDE trainable and maximize n_CQ w/ SGD! We use a basis of terms from u_x => u_xxx^3, and do 5000 runs. Here’s the 3D PCA of our solutions:

4/7
3/N We find that most of our solutions are a linear combination of 4 families of PDEs, one of which is a form of the KdV eq., and 3 which are (afaik) new to the literature! Here, we confirm that these newly minted integrable PDEs have at least one CQ:

5/7
4/N It’s great that AI helped us find some new integrable PDEs, but it’s up to human scientists to interpret and analyze these findings. We focus on a reduced version of the red PDE, u_t=u_x^3, and find it exhibits breaking, infinite CQs, and power law decay to a triangular wave!

6/7
5/N We hope physicists use OptPDE to discover more novel integrable PDEs to model complex phenomena.
Notably, OptPDE requires AI and human scientists to work in tandem, and we hope this paradigm is embraced by the physics community to fully take advantage of modern AI tools

7/7
paper:


To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196

Spoiler: larger images

 

[bnew]

AI explanation by claude 3 haiku:


This paper is about using a computer program to help find special types of math equations that are really useful in physics and engineering. These special equations are called "integrable systems."

Integrable systems have a special property - they have a lot of "conserved quantities." Conserved quantities are things about the equation that stay the same over time, no matter how the equation changes. This makes integrable systems very predictable and controllable, which is why scientists and engineers are really interested in finding them.

The problem is, integrable systems are extremely rare and hard to find using traditional methods. The researchers in this paper thought, "Maybe we can use a computer program to help us find these special equations?"

So they developed two main parts to their approach:

1. CQFinder:
This is a computer program that can take any math equation (specifically, a partial differential equation or PDE) and figure out how many conserved quantities it has. It does this by setting up a bunch of math equations and using a technique called "singular value decomposition" to solve them.

2. OptPDE:
This is the main computer program that tries to discover new integrable systems. It takes a general form of a PDE, with a bunch of terms and coefficients. Then it uses optimization techniques to adjust those coefficients in a way that maximizes the number of conserved quantities, as calculated by the CQFinder program.

By running this OptPDE program many times with different starting points, the researchers were able to discover four families of PDEs that have at least one conserved quantity. One of these families was already known, but the other three were completely new!

The researchers took a closer look at one of these new PDE families, called ut = (ux + a^2 uxxx)^3. They found that for a special case where a = 0, this equation has an infinite number of conserved quantities, which is really remarkable.

They also studied how solutions to this equation evolve over time, showing that they start out as wave-like patterns, but then eventually "break" and degrade into simpler linear shapes. The researchers were able to predict when this breaking point would occur and propose a model to explain the behavior after the breaking point.

Overall, this paper demonstrates how a collaboration between computers and human scientists can lead to the discovery of new and interesting mathematical equations that could have important applications in physics and engineering. The computer program generates the hypotheses, while the human scientists provide the domain knowledge and interpretation.

---

Here's a more comprehensive breakdown of the paper in layman's terms:

Introduction:
- Integrable systems are special mathematical equations, particularly partial differential equations (PDEs), that have many conserved properties. This makes them very useful in physics and engineering.
- However, integrable systems are extremely rare and difficult to discover using traditional methods.
- The key question the paper aims to address is: can machine learning be used to discover new integrable systems?

Method:
1. CQFinder:
- This is an algorithm developed by the researchers to find the conserved quantities (CQs) of a given PDE.
- It takes a PDE and a set of basis functions as input, and outputs the number of CQs (nCQ) and their symbolic formulas.
- The algorithm works by setting up a linear system of equations based on the condition that the CQs must be constant over time, and then using singular value decomposition to find the solutions.

2. OptPDE:
- This is the main machine learning algorithm that discovers new integrable PDEs.
- It takes a basis of PDE terms as input, along with the CQ basis used by CQFinder.
- OptPDE then optimizes the coefficients of the PDE basis to maximize the number of CQs (nCQ), as calculated by CQFinder.
- This is done using a smooth approximation of nCQ that allows backpropagation and gradient-based optimization.

Results:
A. Benchmarking CQFinder:
- The researchers show that CQFinder can correctly identify the number and symbolic forms of CQs for well-known integrable PDEs like Burgers, KdV, and Schrödinger equations.

B. OptPDE Discovers Three Novel Integrable Systems:
- By running OptPDE with a general PDE basis and 5000 random initializations, the researchers discover four families of PDEs with at least one CQ.
- One of these families corresponds to the well-known KdV equation, while the other three are novel.
- They analyze one of the novel PDE families in more detail: ut = (ux + a^2 uxxx)^3.

C. Analyzing an AI-discovered System:
- For the special case a = 0 of the novel PDE family, the researchers find it has an infinite number of CQs.
- They study the evolution of this PDE, showing it exhibits wave-like behavior that eventually breaks and degrades into linear components.
- The researchers derive the time at which the wave breaks and propose a phenomenological model to explain the power-law decay of the wave magnitude after breaking.

Conclusion:
- The paper introduces an AI-human collaborative paradigm for discovering integrable systems, where the AI generates hypotheses and the humans provide domain knowledge and interpretation.
- This approach led to the discovery of several novel integrable PDEs, demonstrating the potential of machine learning to accelerate progress in physics and mathematics.
- The researchers hope this work will inspire similar collaborative AI-human schemas for other problems in physics and beyond.

 

[Professor Emeritus]

Title is sorta misleading.

These are math equations, not physics equations. They could potentially have useful applications to physicists, but they don't describe any new physical reality or correlate to existing physical laws in any way. They're basically just additions to a physicist's toolbox.